题目内容
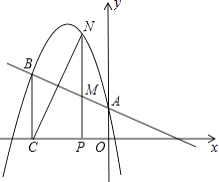
【题目】如图,AB是⊙O的直径,AE平分∠BAF,交⊙O于点E,过点E作直线ED⊥AF,交AF的延长线于点D,交AB的延长线于点C.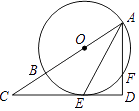
(1)求证:CD是⊙O的切线;
(2)若tanC= ![]() ,⊙O的半径为2,求DE的长.
,⊙O的半径为2,求DE的长.
【答案】
(1)证明:连接OE.
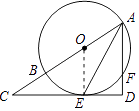
∵OA=OE,
∴∠OAE=∠OEA,
又∵∠DAE=∠OAE,
∴∠OEA=∠DAE,
∴OE∥AD,
∴∠ADC=∠OEC,
∵AD⊥CD,
∴∠ADC=90°,
故∠OEC=90°.
∴OE⊥CD,
∴CD是⊙O的切线
(2)解:∵tanC= ![]() ,
,
∴∠C=30°,
又∵OE=2,
∴OC=4,AC=6,
在Rt△OCE中,tanC= ![]() ,
,
∴CE=2 ![]() ,
,
在Rt△ACD中,cosC= ![]() ,
,
CD=3 ![]()
∴DE=CD﹣CE=3 ![]() ﹣2
﹣2 ![]() =
= ![]() .
.
【解析】(1)连接OE.依据等腰三角形的性质和角平分线的定义可得到∠OEA=∠DAE,从而可证明OE∥AD,然后依据平行线的性质可证∠OEC=90°;
(2)先依据特殊锐角三角函数值可求得∠C=30°,然后可求得AC=6,依据特殊锐角三教函数值可求得CE和CD的长,最后依据DE=CD﹣CE求解即可.
【考点精析】认真审题,首先需要了解角平分线的性质定理(定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上),还要掌握解直角三角形(解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法))的相关知识才是答题的关键.

练习册系列答案
相关题目