Question

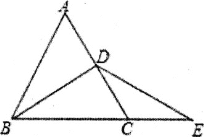
【题目】如图，在等边△ABC中，O为BC边上一点，E为AC边上一点，且∠ADE=60°，BD=3．CE=2，则AB的长为 ．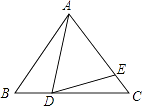

Answer 1

【答案】9
【解析】解：∵△ABC是等边三角形，

∴∠B=∠C=60°，AB=BC；

∴CD=BC﹣BD=AB﹣3；

∴∠BAD+∠ADB=120°，

∵∠ADE=60°，

∴∠ADB+∠EDC=120°，

∴∠DAB=∠EDC，

又∵∠B=∠C=60°，

∴△ABD∽△DCE；

∴ ，

即 = ，

解得AB=9．

所以答案是：9．

【考点精析】本题主要考查了三角形的外角和等边三角形的性质的相关知识点，需要掌握三角形一边与另一边的延长线组成的角，叫三角形的外角；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角；等边三角形的三个角都相等并且每个角都是60°才能正确解答此题．