��Ŀ����
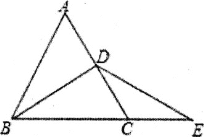
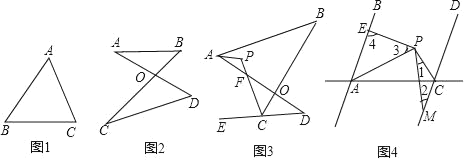
����Ŀ����1����ͼ����֤����A+��B+��C��180��
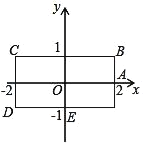
��2����ͼ��ͼ�����ǰ�����Ϊ��8����������֤����A+��B����C+��D
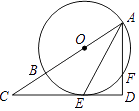
��3����ͼ��E��DC���ӳ����ϣ�APƽ�֡�BAD��CPƽ�֡�BCE�������P���B����D֮��Ĺ�ϵ����֤��
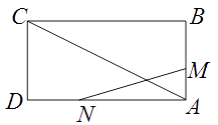
��4����ͼ��AB��CD��PAƽ�֡�BAC��PCƽ�֡�ACD������P��PM��PE��CD��M����AB��E����١�1+��2+��3+��4���䣻�ڡ�3+��4����1����2���䣬ѡ����ȷ�IJ�����֤����
���𰸡���1������������2������������3����P��90��+![]() ����B+��D������4����3+��4����1����2������ȷ�����ɼ�����
����B+��D������4����3+��4����1����2������ȷ�����ɼ�����
��������
��1���ӳ�BC��D������C��CE��BA��������ֱ��ƽ�У�ͬλ����ȿɵá�B����1����ֱ��ƽ�У��ڴ�����ȿɵá�A����2���ٸ���ƽ�ǵĶ�����ʽ�������ɵ�֤��
��2�������������ڽǺͶ�������֤����
��3�����ݣ�2���Ľ��ۡ�B+��BAD����D+��BCD����PAD+��P����D+��PCD��Ȼ���������ɵý⣻
��4����PQ��AB������ƽ�������ʵõ�PQ��CD�����APQ��180������3����4����5����2�����ڡ�APQ+��5+��1��90������180������3����4+��2+��1��90���������õ���3+��4����1����2��90����
��1��֤������ͼ1���ӳ�BC��D������C��CE��BA��
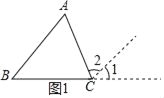
��BA��CE��
���B����1��
��A����2��
�֡ߡ�BCD����BCA+��2+��1��180����
���A+��B+��ACB��180����
��2��֤������ͼ2������AOB�У���A+��B+��AOB��180����

����COD����C+��D+��COD��180����
�ߡ�AOB����COD��
���A+��B����C+��D��
��3����ͼ3��
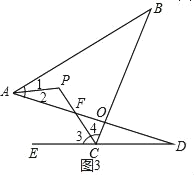
��APƽ�֡�BAD��CPƽ�֡�BCD����ǡ�BCE��
���1����2����3����4��
�ߣ���1+��2��+��B����180����2��3��+��D��
��2+��P����180������3��+��D��
��2��P��180��+��D+��B��
���P��90��+![]() ����B+��D����
����B+��D����
��4���ڡ�3+��4����1����2������ȷ��
�������£�
��PQ��AB����ͼ4��
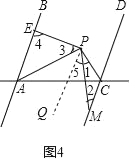
��AB��CD��
��PQ��CD��
��AB��PQ�á�APQ+��3+��4��180��������APQ��180������3����4��
��PQ��CD�á�5����2��
�ߡ�APQ+��5+��1��90����
��180������3����4+��2+��1��90����
���3+��4����1����2��90����

 ��Կ���Ծ�ϵ�д�
��Կ���Ծ�ϵ�д�����Ŀ����֪����Rt��ABC�У���C��90�㣬��A����B����C�ĶԱ߷ֱ�Ϊa��b��c�����ABC�����ΪS���ܳ�Ϊl��
��1�������
����a��b��c |
|
|
3��4��5 | 2 | |
5��12��13 | 4 | |
8��15��17 | 6 |
��2�����![]() ���۲��ϱ����룺
���۲��ϱ����룺 ![]() (�ú���m�Ĵ���ʽ��ʾ)��
(�ú���m�Ĵ���ʽ��ʾ)��
��3��֤����2���еĽ��ۣ�