题目内容
 16、如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE.
16、如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE.(1)写出∠AOC与∠BOD的大小关系:
相等
,判断的依据是等角的补角相等
;(2)若∠COF=35°,求∠BOD的度数.
分析:(1)能够发现要找的两个角都和∠BOC互补,根据等角的补角相等即可说明;
(2)首先根据直角由已知角求得它的余角,再根据角平分线的概念求得∠AOE,再利用角的关系求得∠AOC,根据上述结论,即求得了∠BOD.
(2)首先根据直角由已知角求得它的余角,再根据角平分线的概念求得∠AOE,再利用角的关系求得∠AOC,根据上述结论,即求得了∠BOD.
解答:解:(1)相等,等角的补角相等;
(2)∵∠COE是直角,∠COF=35°
∴∠EOF=55°
又OF平分∠AOE,∴∠AOE=110°
∴∠AOC=20°
∴∠BOD=∠AOC=20°.
故答案为相等、等角的补角相等、20°.
(2)∵∠COE是直角,∠COF=35°
∴∠EOF=55°
又OF平分∠AOE,∴∠AOE=110°
∴∠AOC=20°
∴∠BOD=∠AOC=20°.
故答案为相等、等角的补角相等、20°.
点评:(1)理解邻补角的概念,掌握等角的补角相等的性质;
(2)正确求得一个角的余角,熟练运用角平分线表示角之间的倍分关系,再根据角之间的和差关系进行计算.
(2)正确求得一个角的余角,熟练运用角平分线表示角之间的倍分关系,再根据角之间的和差关系进行计算.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
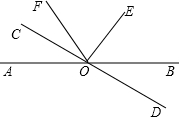 如图,已知直线AB和CD相交于O点,∠DOE是直角,OF平分∠AOE,∠BOD=22°,求∠COF的度数.
如图,已知直线AB和CD相交于O点,∠DOE是直角,OF平分∠AOE,∠BOD=22°,求∠COF的度数.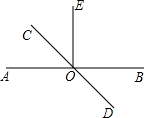 (2013•奉贤区二模)如图,已知直线AB和CD相交于点O,OE⊥AB,∠AOD=128°,则∠COE的度数是
(2013•奉贤区二模)如图,已知直线AB和CD相交于点O,OE⊥AB,∠AOD=128°,则∠COE的度数是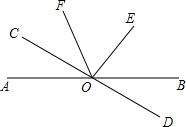 (1)已知一个角的余角是这个角的补角的
(1)已知一个角的余角是这个角的补角的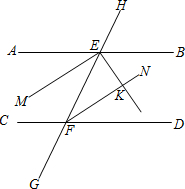 如图,已知直线AB和直线CD被直线GH所截,交点分别为E、F点,且AB∥CD.
如图,已知直线AB和直线CD被直线GH所截,交点分别为E、F点,且AB∥CD.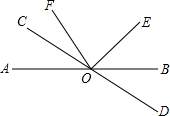 如图,已知直线AB和CD相交于O点,∠COE是直角,OF平分∠AOE,∠COF=34°,则∠BOD的大小为
如图,已知直线AB和CD相交于O点,∠COE是直角,OF平分∠AOE,∠COF=34°,则∠BOD的大小为