题目内容
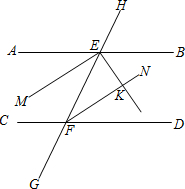 如图,已知直线AB和直线CD被直线GH所截,交点分别为E、F点,且AB∥CD.
如图,已知直线AB和直线CD被直线GH所截,交点分别为E、F点,且AB∥CD.(1)若ME是∠AEF的平分线,FN是∠EFD的平分线,则EM与FN平行吗?若平行,试说明理由.
(2)若EK是∠BEF的平分线,则EK和FN垂直吗?说明理由.
分析:(1)EM与FN平行,理由为:由ME与FN分别为角平分线,利用角平分线定义得到∠MEF=
∠AEF,∠EFN=
∠EFD,再由AB与CD平行,利用两直线平行内错角相等得到一对角相等,等量代换得到一对内错角相等,利用内错角相等两直线平行即可得证;
(2)EK与FN垂直,理由为:由AB与CD平行,利用两直线平行同旁内角互补得到一对角互补,再由角平分线定义得到∠FEK=
∠FEB,∠EFN=
∠EFD,等量代换得到∠FEK+∠EFN=90°,即可确定出EK与FN垂直.
| 1 |
| 2 |
| 1 |
| 2 |
(2)EK与FN垂直,理由为:由AB与CD平行,利用两直线平行同旁内角互补得到一对角互补,再由角平分线定义得到∠FEK=
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)EM∥FN,理由为:
∵ME是∠AEF的平分线,FN是∠EFD的平分线,
∴∠MEF=
∠AEF,∠EFN=
∠EFD,
又∵AB∥CD,
∴∠AEF=∠EFD,
∴∠MEF=∠EFN,
∴EM∥FN;
(2)EK⊥FN,理由为:
∵AB∥CD,
∴∠BEF+∠EFD=180°,
又∵EK是∠BEF的平分线,FN是∠EFD的平分线,
∴∠FEK=
∠BEF,∠EFN=
∠EFD,
∴∠FEK+∠EFN=90°,
∴∠EKF=90°即EK⊥FN.
∵ME是∠AEF的平分线,FN是∠EFD的平分线,
∴∠MEF=
| 1 |
| 2 |
| 1 |
| 2 |
又∵AB∥CD,
∴∠AEF=∠EFD,
∴∠MEF=∠EFN,
∴EM∥FN;
(2)EK⊥FN,理由为:
∵AB∥CD,
∴∠BEF+∠EFD=180°,
又∵EK是∠BEF的平分线,FN是∠EFD的平分线,
∴∠FEK=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠FEK+∠EFN=90°,
∴∠EKF=90°即EK⊥FN.
点评:此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.

练习册系列答案
相关题目
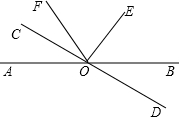 如图,已知直线AB和CD相交于O点,∠DOE是直角,OF平分∠AOE,∠BOD=22°,求∠COF的度数.
如图,已知直线AB和CD相交于O点,∠DOE是直角,OF平分∠AOE,∠BOD=22°,求∠COF的度数.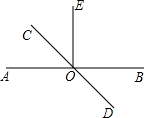 (2013•奉贤区二模)如图,已知直线AB和CD相交于点O,OE⊥AB,∠AOD=128°,则∠COE的度数是
(2013•奉贤区二模)如图,已知直线AB和CD相交于点O,OE⊥AB,∠AOD=128°,则∠COE的度数是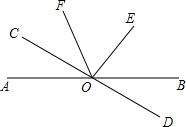 (1)已知一个角的余角是这个角的补角的
(1)已知一个角的余角是这个角的补角的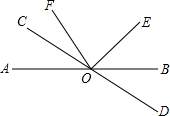 如图,已知直线AB和CD相交于O点,∠COE是直角,OF平分∠AOE,∠COF=34°,则∠BOD的大小为
如图,已知直线AB和CD相交于O点,∠COE是直角,OF平分∠AOE,∠COF=34°,则∠BOD的大小为