题目内容
 (1)已知一个角的余角是这个角的补角的
(1)已知一个角的余角是这个角的补角的| 1 | 4 |
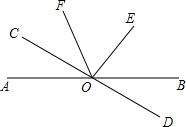
(2)如图,已知直线AB和CD相交于O点,CO⊥OE,OF 平分∠AOE,∠COF=26°,求∠BOD的度数.
分析:(1)设这个角为x度,表示出这个角的余角是(90-x)度,补角是(180-x)度,然后列出方程求解即可;
(2)根据垂直的定义可得∠COE=90°,然后求出∠EOF,再根据角平分线的定义求出∠AOF,然后求出∠AOC,再根据对顶角相等解答即可.
(2)根据垂直的定义可得∠COE=90°,然后求出∠EOF,再根据角平分线的定义求出∠AOF,然后求出∠AOC,再根据对顶角相等解答即可.
解答:解:(1)设这个角为x度,则这个角的余角是(90-x)度,补角是(180-x)度,
由题意得:90-x=
(180-x),
解得x=60,
所以,这个角是60°,这个角的余角是30°,这个角的补角是120°;
(2)∵CO⊥OE,
∴∠COE=90°,
又∵∠COF=26°,
∠EOF=90°-26°=64°,
∵OF平分∠AOE,
∴∠AOF=EOF=64°,
∴∠AOC=64°-26°=38°,
∵∠AOC与∠BOD是对顶角,
∴∠BOD=38°.
由题意得:90-x=
| 1 |
| 4 |
解得x=60,
所以,这个角是60°,这个角的余角是30°,这个角的补角是120°;
(2)∵CO⊥OE,
∴∠COE=90°,
又∵∠COF=26°,
∠EOF=90°-26°=64°,
∵OF平分∠AOE,
∴∠AOF=EOF=64°,
∴∠AOC=64°-26°=38°,
∵∠AOC与∠BOD是对顶角,
∴∠BOD=38°.
点评:本题考查了余角和补角的定义,角平分线的定义,是基础题,(1)设出未知数列出方程是解题的关键,(2)准确识图,找出各角度之间的关系是解题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目

 多1°,求这个角的度数;
多1°,求这个角的度数;