题目内容
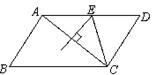
如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF;
(2)在图1中,若G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
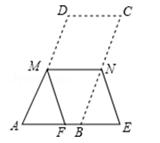
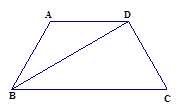
如图2,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC=6,E是AB上一点,且∠DCE=45°,BE=2,求DE的长.

(1)求证:CE=CF;
(2)在图1中,若G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图2,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC=6,E是AB上一点,且∠DCE=45°,BE=2,求DE的长.
|
|

(1)见解析
(2)见解析
(3)DE=5.

(2)见解析
(3)DE=5.

试题分析:(1)由条件直接证明三角形全等就可以得出CE=CF.
(2)由条件和(1)的结论可以证明三角形ECG全等三角形FCG,可以得出EG=FG,可以得出GE=BE+GD.
(3)过点C作CG⊥AD的延长线于点G,在AD的延长线上取点H,使GH=BE,从而运用(2)的结论可以表示出DG,由勾股定理就可以求出DE的值.
点评:熟练掌握正方形的性质和全等三角形的判定与性质,勾股定理的运用及直角梯形的性质是正确解答的基础.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的对角线
的对角线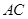 和
和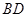 相交于点
相交于点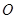 ,过点
,过点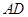 和
和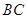 于点E、F,AB=2,BC=4,则图中阴影部分的面积为 .
于点E、F,AB=2,BC=4,则图中阴影部分的面积为 . 
 ABCD的一边长为10,则对角线AC、BD的长可取下列数据中的( )
ABCD的一边长为10,则对角线AC、BD的长可取下列数据中的( )