题目内容
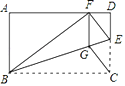
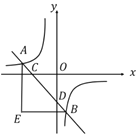
【题目】如图,在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() 分别在
分别在![]() 轴的负半轴、
轴的负半轴、![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在第二象限.将矩形
在第二象限.将矩形![]() 绕点
绕点![]() 顺时针旋转,使点
顺时针旋转,使点![]() 落在
落在![]() 轴上,得到矩形
轴上,得到矩形![]() 与
与![]() 相交于点
相交于点![]() .若经过点
.若经过点![]() 的反比例函数
的反比例函数![]() 的图象交
的图象交![]() 于点
于点![]() 的图象交
的图象交![]() 于点
于点![]()
![]() 则
则![]() 的长为____.
的长为____.
【答案】![]()
【解析】
利用矩形的面积公式得到ABBC=32,再根据旋转的性质得AB=DE,OD=OA,接着利用正切的定义得到tan∠DOE=![]() ,所以DE2DE=32,解得DE=4,于是得到AB=4,OA=8,同样在Rt△OCM中利用正切定义得到MC=2,则M(2,4),易得反比例函数解析式为y=
,所以DE2DE=32,解得DE=4,于是得到AB=4,OA=8,同样在Rt△OCM中利用正切定义得到MC=2,则M(2,4),易得反比例函数解析式为y=![]() ,然后确定N点坐标,最后计算BN的长.
,然后确定N点坐标,最后计算BN的长.
解:∵S矩形OABC=32,
∴ABBC=32,
∵矩形OABC绕点O顺时针旋转,使点B落在y轴上,得到矩形ODEF,
∴AB=DE,OD=OA,
在Rt△ODE中,tan∠DOE=![]() ,即OD=2DE,
,即OD=2DE,
∴DE2DE=32,解得DE=4,
∴AB=4,OA=8,
在Rt△OCM中,∵tan∠COM=![]() ,
,
而OC=AB=4,
∴MC=2,
∴M(2,4),
把M(2,4)代入![]() 中,得k=2×4=8,
中,得k=2×4=8,
∴反比例函数解析式为y=![]() ,
,
当x=8时,y=1,
则N(8,1),
∴BN=41=3.
故答案为3.

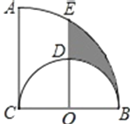
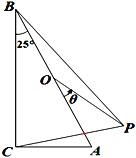
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=25°,O为AB的中点. 将OA绕点O逆时针旋转θ °至OP(0<θ<180),当△BCP恰为轴对称图形时,θ的值为_____________.
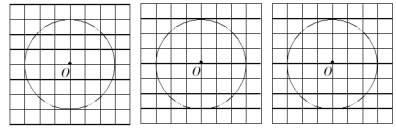
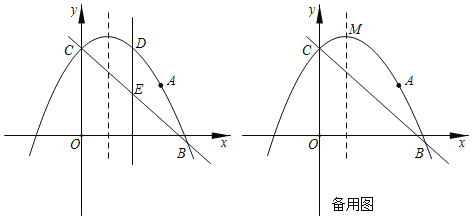
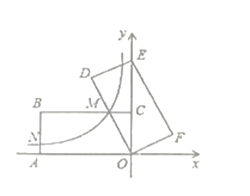
【题目】某“兴趣小组”根据学习函数的经验,对函数y=x+![]() 的图象和性质进行了探究,探究过程如下,请补充完整.
的图象和性质进行了探究,探究过程如下,请补充完整.

(1)函数y=x+![]() 的自变量取值范围是________;
的自变量取值范围是________;
(2)下表是x与y的几组对应值:
x | … | -3 | -2 | -1 | - | - |
|
| 1 | 2 | 3 | … |
y | … | - | - | -2 | - | - |
|
| 2 |
| m | … |
则表中m的值为________;
(3)根据表中数据,在如图所示平面直角坐标xOy中描点,并画出函数的一部分,请画出
(4)观察函数图象:写出该函数的一条性质
(5)进一步探究发现:函数y=x+![]() 图象与直线y=-2只有一交点,所以方程x+
图象与直线y=-2只有一交点,所以方程x+![]() =-2只有1个实数根,若方程x+
=-2只有1个实数根,若方程x+![]() =k(x<0)有两个不相等的实数根,则k的取值范围是 ________.
=k(x<0)有两个不相等的实数根,则k的取值范围是 ________.