题目内容
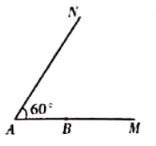
【题目】有两张完全重合的矩形纸片,将其中一张绕点![]() 顺时针旋转
顺时针旋转![]() 后得到矩形
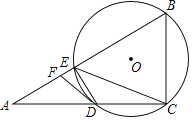
后得到矩形![]() (如图1),连接
(如图1),连接![]() ,
,![]() ,若
,若![]() ,
,![]() .
.

(1)试探究线段![]() 与线段
与线段![]() 的数量关系和位置关系,并说明理由;
的数量关系和位置关系,并说明理由;
(2)把![]() 与
与![]() 剪去,将
剪去,将![]() 绕点
绕点![]() 顺时针旋转得
顺时针旋转得![]() ,边
,边![]() 交
交![]() 于点
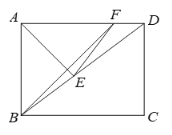
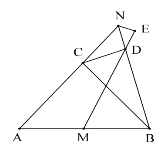
于点![]() (如图2),设旋转角为
(如图2),设旋转角为![]() ,当
,当![]() 为等腰三角形时,求
为等腰三角形时,求![]() 的度数;
的度数;
(3)若将![]() 沿
沿![]() 方向平移得到
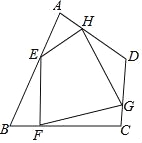
方向平移得到![]() (如图3),
(如图3),![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,当
,当![]() 时,求平移的距离.
时,求平移的距离.
【答案】(1)![]() ,
,![]() ,理由见解析;(2)
,理由见解析;(2)![]() 或
或![]() ;(3)平移的距离是
;(3)平移的距离是![]()
【解析】
(1)有两张完全重合的矩形纸片,将其中一张绕点A顺时针旋转90°后得到矩形AMEF(如图1),得BD=MF,△BAD≌△MAF,推出BD=MF,∠ADB=∠AFM=30°,进而可得∠DNM的大小.
(2)分两种情形讨论①当AK=FK时,②当AF=FK时,根据旋转的性质得出结论.
(3)求平移的距离是A2A的长度.在矩形PNA2A中,A2A=PN,只要求出PN的长度就行.用△DPN∽△DAB得出对应线段成比例,即可得到A2A的大小.
(1)解:![]() ,
,![]() .
.
延长![]() 交
交![]() 于点
于点![]() ,
,

根据旋转的性质得:AB=AM,AD=AF,∠BAD=∠MAF=90°
∴![]() .
.
∴![]() ,
,![]() .
.
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
(2)解:如图2,

①当![]() 时,
时,![]() ,
,
则![]() ,即
,即![]() ;
;
②当![]() 时,
时,![]() ,
,
∴![]() ,即
,即![]() ;
;
∴![]() 的度数为
的度数为![]() 或
或![]()
(3)如图3,
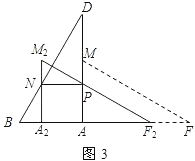
由题意得矩形![]() .设
.设![]() ,则
,则![]() ,
,
在![]() 中,∵
中,∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴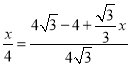 ,
,
解得![]() .即
.即![]() .
.
答:平移的距离是![]() .
.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目