题目内容
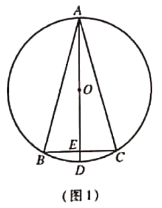
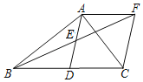
【题目】如图,在等边△ABC中,BD=CE,连接AD、BE交于点F.
(1)求∠AFE的度数;
(2)求证:ACDF=BDBF;
(3)连接FC,若CF⊥AD时,求证:BD=![]() DC.
DC.
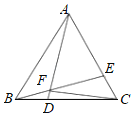
【答案】(1)60°;(2)证明见解析;(3)证明见解析
【解析】
(1)证明△ABD≌△BCE(SAS),得出∠BAD=∠CBE,则∠BFD=∠AFE=∠ABC=60°;
(2)证明△ADB∽△BDF,得出![]() ,由AB=AC可得出结论;
,由AB=AC可得出结论;
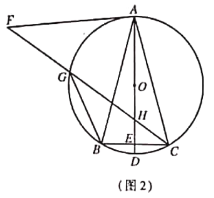
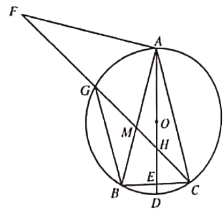
(3)延长BE至H,使FH=AF,连接AH,CH,证明△BAF≌△CAH(SAS),得出∠ABF=∠ACH,CH=BF,可证明AF∥CH,得出![]() ,进而即可得出答案.
,进而即可得出答案.
解:(1)∵△ABC是等边三角形,
∴AB=AC=BC,∠ABD=∠BCE=60°,
在△ABD和△BCE中,
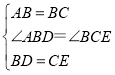 ,
,
∴△ABD≌△BCE(SAS),
∴∠BAD=∠CBE,
∵∠ADC=∠CBE+∠BFD=∠BAD+∠ABC,
∴∠BFD=∠AFE=∠ABC=60°;
(2)证明:由(1)知∠BAD=∠DBF,
又∵∠ADB=∠BDF,
∴△ADB∽△BDF,
∴![]() ,
,
又AB=AC,
∴![]() ,
,
∴ACDF=BDBF;
(3)证明:延长BE至H,使FH=AF,连接AH,CH,
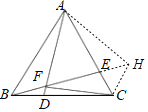
由(1)知∠AFE=60°,∠BAD=∠CBE,
∴△AFH是等边三角形,
∴∠FAH=60°,AF=AH,
∴∠BAC=∠FAH=60°,
∴∠BAC﹣∠CAD=∠FAH﹣∠CAD,
即∠BAF=∠CAH,
在△BAF和△CAH中,
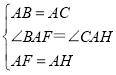 ,
,
∴△BAF≌△CAH(SAS),
∴∠ABF=∠ACH,CH=BF,
又∵∠ABC=∠BAC,∠BAD=∠CBE,
∴∠ABC﹣∠CBE=∠BAC﹣∠BAD,
即∠ABF=∠CAF,
∴∠ACH=∠CAF,
∴AF∥CH,
∵∠AFC=90°,∠AFE=60°,
∴CF⊥CH,∠CFH=30°,
∴FH=2CH,
∴FH=2BF,
∵FD∥CH,
∴![]() ,
,
∴BD=![]() DC.
DC.

 巧学巧练系列答案
巧学巧练系列答案