题目内容
【题目】如图所示的曲边三角形可按下述方法作出：作等边三角形
；分别以点
，
，
为圆心，以
的长为半径作
，
，
．三段弧所围成的图形就是一个曲边三角形，如果一个曲边三角形的周长为
，那么这个曲边三角形的面积是___________．
【答案】
【解析】
先根据周长，利用弧长公式，可求得等边△ABC的边长，然后用以A、B、C为圆心的三个扇形面积和减2个△ABC的面积解得．
∵曲边三角形的周长为
∴一条曲边的长为：
π
∵△ABC是等边三角形，∴∠A=∠B=∠C=60°，即一段弧对应的圆心角为60°
∴
π
解得：r=2，即AB=BC=AC=2
如下图，阴影部分是以A为圆心的扇形
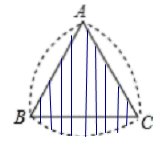
面积为：
π
同样以点B、C为圆心的扇形面积也为：π
则这三个扇形面积和为：2π
发现，三个扇形面积相加，中间的△ABC的面积计算了3次，我们还需要减去2次
如下图，过点A作BC的垂线，交BC于点D
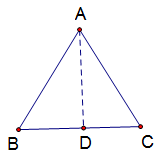
∵等边△ABC的边长为2
∴CD=1，AD=
∴△ABC的面积=
=
∴曲边三角形的面积=2π-2
故答案为：
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
相关题目
