题目内容
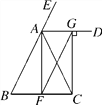
【题目】如图,∠CAE是△ABC的外角,AD平分∠EAC,且AD∥BC.过点C作CG⊥AD,垂足为G,AF是BC边上的中线,连接FG.
(1)求证:AC=FG;
(2)当AC⊥FG时,△ABC应是怎样的三角形?为什么?
【答案】(1)证明见解析;(2)当AC⊥FG时,△ABC是等腰直角三角形,理由见解析.
【解析】试题分析:(1)先根据题意推理出四边形AFCG是矩形,然后根据矩形的性质得到对角线相等;
(2)由(1)的结论和AC⊥FG得到四边形AFCG是正方形,然后即可得到△ABC是等腰直角三角形.
试题解析:
(1)∵AD平分∠EAC,且AD∥BC,
∴∠ABC=∠EAD=∠CAD=∠ACB,
∴AB=AC.
∵AF是BC边上的中线,
∴AF⊥BC.
∵CG⊥AD,AD∥BC,
∴CG⊥BC,
∴AF∥CG,
∴四边形AFCG是平行四边形.
∵∠AFC=90°,
∴四边形AFCG是矩形.
∴AC=FG.
(2)当AC⊥FG时,△ABC是等腰直角三角形.理由如下:
∵四边形AFCG是矩形,AC⊥FG,
∴四边形AFCG是正方形,∠ACB=45°.
∵AB=AC,
∴△ABC是等腰直角三角形.

练习册系列答案
相关题目