题目内容
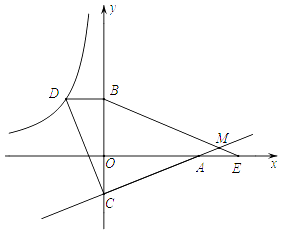
【题目】如图,已知点D在反比例函数y= ![]() 的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=
的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC= ![]() .
.
(1)求反比例函数y= ![]() 和直线y=kx+b的解析式;
和直线y=kx+b的解析式;
(2)连接CD,试判断线段AC与线段CD的关系,并说明理由;
(3)点E为x轴上点A右侧的一点,且AE=OC,连接BE交直线CA与点M,求∠BMC的度数.
【答案】
(1)
解:∵A(5,0),
∴OA=5.
∵ ![]() ,
,
∴ ![]() ,解得OC=2,
,解得OC=2,
∴C(0,﹣2),
∴BD=OC=2,
∵B(0,3),BD∥x轴,
∴D(﹣2,3),
∴m=﹣2×3=﹣6,
∴ ![]() ,
,
设直线AC关系式为y=kx+b,
∵过A(5,0),C(0,﹣2),
∴ ![]() ,解得
,解得 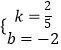 ,
,
∴ ![]()
(2)
解:∵B(0,3),C(0,﹣2),
∴BC=5=OA,
在△OAC和△BCD中

∴△OAC≌△BCD(SAS),
∴AC=CD,
∴∠OAC=∠BCD,
∴∠BCD+∠BCA=∠OAC+∠BCA=90°,
∴AC⊥CD
(3)
解:∠BMC=45°.
如图,连接AD,
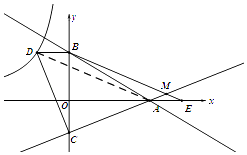
∵AE=OC,BD=OC,AE=BD,
∴BD∥x轴,
∴四边形AEBD为平行四边形,
∴AD∥BM,
∴∠BMC=∠DAC,
∵△OAC≌△BCD,
∴AC=CD,
∵AC⊥CD,
∴△ACD为等腰直角三角形,
∴∠BMC=∠DAC=45°
【解析】(1)由A点坐标可求得OA的长,再利用三角函数的定义可求得OC的长,可求得C、D点坐标,再利用待定系数法可求得直线AC的解析式;(2)由条件可证明△OAC≌△BCD,再由角的和差可求得∠OAC+∠BCA=90°,可证得AC⊥CD;(3)连接AD,可证得四边形AEBD为平行四边形,可得出△ACD为等腰直角三角形,则可求得答案.

练习册系列答案
相关题目