��Ŀ����
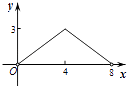
����Ŀ����һ����ֱ�Ĺ�·����A��B���أ��������г���A�ص�B�أ��������г���B�ص�A�ڣ�����A�غ�������ԭ·���أ���ͼ�Ǽס���������B�صľ���y��km������ʻʱ��x��h��֮��ĺ���ͼ����ͼ�����������⣺
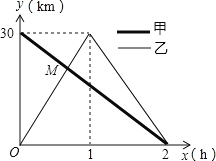
��1��A��B����֮��ľ��룺 km��
��2�����ٶ�Ϊ km/h���ҵ��ٶ�Ϊ30km/h��
��3����M������Ϊ ��
��4������B�صľ���y��km������ʻʱ��x��h��֮��ĺ�����ϵʽ������д���Ա�����ȡֵ��Χ����
���𰸡���1��30����2��15����3����![]() ��20������4��y=-15x+30��
��20������4��y=-15x+30��
��������
�����������1�����ݺ���ͼ��Ϳ��Եó�A��B���صľ��룻
��2�����ݺ���ͼ��Ӧ��ʱ�伴��������ҵ��ٶȣ�
��3�����ݺ���ͼ��Ӧ��ʱ�����������ҵ��ٶȣ��Ϳ����������ʱ�䣬�Ϳ����������B�صľ�����ó�������M�����ꣻ
��4�������B�صľ���y��km������ʻʱ��x��h���ĺ�����ϵʽΪy=kx+b���ѣ�0��20������2��0�����뼴�ɽ��
�����������1���ɺ���ͼ��
A��B���صľ���Ϊ30ǧ�ף�
��A��B���صľ���Ϊ30ǧ�ף�
��2���ɺ���ͼ��
���ٶ�Ϊ��30��2=15ǧ��/ʱ��
�ҵ��ٶ�Ϊ��30��1=30ǧ��/ʱ��
��3������������ʱ��Ϊ��30�£�15+30��=![]() Сʱ��
Сʱ��
����ʱ���뿪B�صľ���Ϊ��![]() ��30=20ǧ�ף�
��30=20ǧ�ף�
��M��![]() ��20����
��20����
��ʾ![]() Сʱʱ������������ʱ����B��20ǧ�ף�
Сʱʱ������������ʱ����B��20ǧ�ף�
��4���裺y=kx+b��
���������![]()
���k=-15��
������������ϵʽΪy=-15x+30��