Question

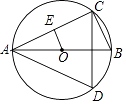
【题目】已知Rt△AEC中，∠E=90°，请按如下要求进行操作和判断：

（1）尺规作图：作△AEC的外接圆⊙O，并标出圆心O（不写画法）；
（2）延长CE，在CE的延长线上取点B，使EB=EC，连结AB，设AB与⊙O的交点为D（标出字母B、D），判断：图中 与 相等吗？请说明理由．

Answer 1

【答案】
（1）解：如图所示，⊙O即为所求；

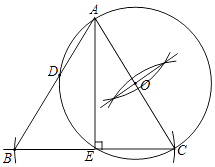
（2）解：延长CE，在CE的延长线上取点B，使EB=EC，连结AB，则△AEB即为所求，

∵BE=EC，AE=AE，AE⊥BC，

∴△AEC≌△AEB（SAS），

∴∠CAE=∠DAE，

∴ 与 相等

【解析】（1）先作出AC的中垂线，交AC于O，再以O为圆心，AO的长为半径画圆即可；（2）延长CE，在CE的延长线上取点B，使EB=EC，连结AB，先判定△AEC≌△AEB（SAS），得出∠CAE=∠DAE即可得出结论．