题目内容
【题目】如图，一次函数y=x+b的图象与反比例函数y= 
（k为常数，k≠0）的图象交于点A（﹣1，4）和点B（a，1）． 
（1）求反比例函数的表达式和a、b的值；
（2）若A、O两点关于直线l对称，请连接AO，并求出直线l与线段AO的交点坐标．
【答案】
（1）
解：∵点A（﹣1，4）在反比例函数y= 
（k为常数，k≠0）的图象上，
∴k=﹣1×4=﹣4，
∴反比例函数解析式为y=﹣ 
．
把点A（﹣1，4）、B（a，1）分别代入y=x+b中，
得： 
，解得： 
（2）
解：连接AO，设线段AO与直线l相交于点M，如图所示．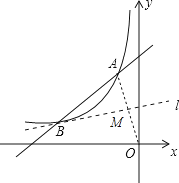
∵A、O两点关于直线l对称，
∴点M为线段OA的中点，
∵点A（﹣1，4）、O（0，0），
∴点M的坐标为（﹣ 
，2）．
∴直线l与线段AO的交点坐标为（﹣ ，2）
【解析】（1）由点A的坐标结合反比例函数图象上点的坐标特征，即可求出k值，从而得出反比例函数解析式；再将点A、B坐标分别代入一次函数y=x+b中得出关于a、b的二元一次方程组，解方程组即可得出结论；
（2）连接AO，设线段AO与直线l相交于点M．由A、O两点关于直线l对称，可得出点M为线段AO的中点，再结合点A、O的坐标即可得出结论．本题考查了反比例函数与一次函数的交点问题、待定系数法求函数解析式、解二元一次方程组以及中点坐标公式，解题的关键是：（1）由点的坐标利用待定系数法求函数系数；（2）得出点M为线段AO的中点．本题属于基础题，难度不大，解决该题型题目时，巧妙的利用了中点坐标公式降低了难度．
【考点精析】解答此题的关键在于理解解二元一次方程组的相关知识，掌握二元一次方程组：①代入消元法；②加减消元法，以及对确定一次函数的表达式的理解，了解确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法．
