题目内容
 如图,AB是⊙O的切线,A为切点,AC是⊙O的弦,过O作OH⊥AC于点H.若OH=2,AB=12,BO=13.
如图,AB是⊙O的切线,A为切点,AC是⊙O的弦,过O作OH⊥AC于点H.若OH=2,AB=12,BO=13.
求:(1)⊙O的半径;
(2)sin∠OAC的值;
(3)弦AC的长.(结果保留两个有效数字)
解:(1)∵AB是⊙O的切线,
∴∠OAB=90°,
∴AO2=OB2-AB2,
∴OA=5;
(2)∵OH⊥AC,
∴∠OHA=90°,
∴sin∠OAC=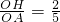 ;
;
(3)∵OH⊥AC,
∴AH2=AO2-OH2,AH=CH,
∴AH2=25-4=21,
∴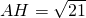 ,
,
∴AC=2AH=2 ≈9.2.
≈9.2.
分析:(1)根据切线的性质,△AOB为直角三角形,根据勾股定理即可求得;
(2)在第1问的基础上,根据垂径定理,即可求得;
(3)在第2问的基础上,求出AH,即可求出AC.
点评:此题主要考查切线性质、垂径定理、勾股定理的基本应用,三者结合应用解答此类问题即可迎刃而解.
∴∠OAB=90°,
∴AO2=OB2-AB2,
∴OA=5;
(2)∵OH⊥AC,
∴∠OHA=90°,
∴sin∠OAC=
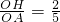 ;
;(3)∵OH⊥AC,
∴AH2=AO2-OH2,AH=CH,
∴AH2=25-4=21,
∴
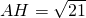 ,
,∴AC=2AH=2
 ≈9.2.
≈9.2.分析:(1)根据切线的性质,△AOB为直角三角形,根据勾股定理即可求得;
(2)在第1问的基础上,根据垂径定理,即可求得;
(3)在第2问的基础上,求出AH,即可求出AC.
点评:此题主要考查切线性质、垂径定理、勾股定理的基本应用,三者结合应用解答此类问题即可迎刃而解.

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 12、已知,如图,AB是⊙O的直径,DC切⊙O于点C,AB=2BC,则∠BCD=
12、已知,如图,AB是⊙O的直径,DC切⊙O于点C,AB=2BC,则∠BCD= 如图,AB是⊙O的直径,点C在AB的延长线上,CD切⊙O于点D,过点D作DF⊥AB于点E,交⊙O于点F,OE=1cm,DF=2cm,则CB的长为( )
如图,AB是⊙O的直径,点C在AB的延长线上,CD切⊙O于点D,过点D作DF⊥AB于点E,交⊙O于点F,OE=1cm,DF=2cm,则CB的长为( )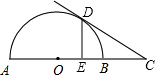
 21、如图,AB是⊙O的直径,AC是弦,直线CE和⊙O切于点C,AD⊥CE,垂足为D.求证:AC平分∠BAD.
21、如图,AB是⊙O的直径,AC是弦,直线CE和⊙O切于点C,AD⊥CE,垂足为D.求证:AC平分∠BAD. 如图,AB是半圆的直径,直线MN切半圆于点C,AM⊥MN,BN⊥MN,如果AM=a,BN=b,那么半圆的直径为
如图,AB是半圆的直径,直线MN切半圆于点C,AM⊥MN,BN⊥MN,如果AM=a,BN=b,那么半圆的直径为