题目内容
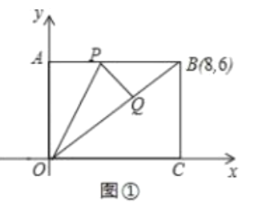
【题目】将矩形纸片放![]() 在平面直角坐标系中,
在平面直角坐标系中,![]() 为坐标原点,点
为坐标原点,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,点
轴上,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 是边
是边![]() 上的-一个动点,将
上的-一个动点,将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 处.
处.
![]() 如图①.当点
如图①.当点![]() 恰好落在
恰好落在![]() 上时,求点
上时,求点![]() 的坐标;
的坐标;
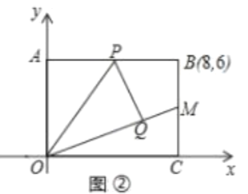
(2)如图②,当点![]() 是
是![]() 中点时,直线
中点时,直线![]() 交
交![]() 于
于![]() 点,
点,
![]() 求证:
求证:![]() ;
;
![]() 求点
求点![]() 的坐标.
的坐标.
【答案】(1)P(3,6);(2) (a)见解析; (b) ![]()
【解析】
(1)根据点B的坐标,可求得OB的长,再利用![]() 得出PB的长,从而得出点P的坐标;
得出PB的长,从而得出点P的坐标;
(2)(a)证![]() 即可得MB=MQ;
即可得MB=MQ;
(b)如下图,设![]() 在
在![]() 中,利用勾股定理可求得m的值,再利用
中,利用勾股定理可求得m的值,再利用![]() 可求得QN和QO的值,从而得到点Q的坐标.
可求得QN和QO的值,从而得到点Q的坐标.
(1)![]() 点
点![]() 的坐标是
的坐标是![]()
![]()
在![]() 中,
中,![]()
根据题意,![]() ,
,![]()
又![]()
![]()
![]()
![]()
![]()
![]()
![]()
(2)(a)连接![]()

根据题意,![]() .
.
![]() 点
点![]() 是
是![]() 中点,
中点,
![]()
![]()
![]() ,
,
![]()
![]()
(b)如图,过点![]() 作
作![]() 轴于点
轴于点![]()

设![]() 则由
则由![]() 知
知![]()
根据题意,知![]()
![]() .
.
在![]() 中,
中,![]()
即![]() ,解得
,解得![]()
![]()
![]() 四边形
四边形![]() 是矩形,
是矩形,
![]()
![]() 轴于点
轴于点![]()
![]()
![]()
![]()
![]()
![]()
![]()
得![]()
![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】十九大召开后,某社区开展了“市民对十九大的关注情况”调查,采用随机抽样的方法访问了部分年龄在18周岁以上的城乡居民.小聪根据调查数据绘制了如下不完整的频数分布置表和扇形统计图.请根据图表解答下列问题.
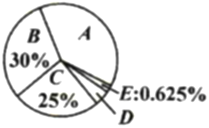
关注情况 | 频数 |
非常关注( | 128 |
比较关注( | |
一般关注( | 80 |
不太关注( | |
不关注( | 2 |
(1)请完成频数分布表空格数据填写;
(2)求“非常关注”部分扇形圆心角的度数;
(3)若该社区18周岁以上居民共有20000人,请估计“比较关注”和“非常关注”的居民共有多少人?