题目内容
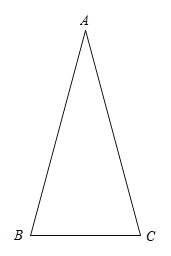
【题目】如图,在△ABC中,∠BAC=30°,AB=AC,将线段AC绕点A逆时针旋转α°(0<α<180),得到线段AD,连接BD,交AC于点P.
(1)当α=90时,
①依题意补全图形;
②求证:PD=2PB;
(2)写出一个α的值,使得PD=![]() PB成立,并证明.
PB成立,并证明.
【答案】(1)①见解析;②见解析;(2)当α=60°(或120°)时,PD=![]() PB,证明见解析
PB,证明见解析
【解析】
(1)当α=90°时,①依题意即可补全图形;
②根据30度角所对直角边等于斜边一半即可证明PD=2PB;
(2)当α的值为60(或120)度时,根据相似三角形的性质即可证明PD=![]() PB成立.
PB成立.
(1)①如图
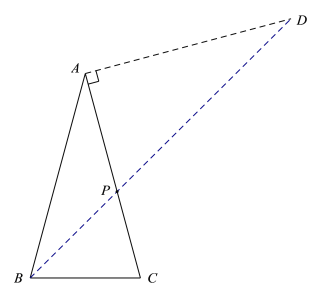
②∵AC=AD,AB=AC
∴AB=AD,∠ABD=∠ADB
又∵∠BAC=30°,∠BAD=90°
∴∠ABD=∠ADB=30°
∴AP=BP
在Rt△APD中,∠ADB=30°
∴PD=2AP
∴PD=2PB
(2)当α=60°(或120°)时,PD=![]() PB
PB
情况Ⅰ:当α=60°时,过点D作DF⊥AC,垂足为点F,过点B作BE⊥AC,垂足为点E,
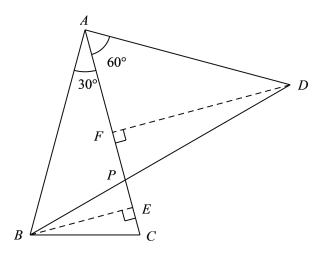
∴DF∥BE
∴△DFP∽△BEP
∴![]()
在Rt△ABE中,∠BAC=30°
∴AC=2BE
在Rt△ADF中,∠CAD=60°
∴AD=![]() DF
DF
又∵AD=AC=AB
∴2BE=![]() DE,即
DE,即![]() BE=DF
BE=DF
∴![]() PB=PD
PB=PD
情况Ⅱ:当α=120°时,过点D作DF⊥AC,交CA的延长线于点F, 过点B作BE⊥AC,垂足为点E,
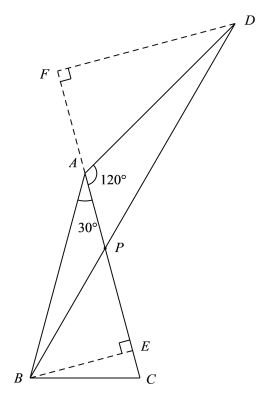
∴DF∥BE
∴△DFP∽△BEP
∴![]()
在Rt△ABE中,∠BAC=30°
∴AC=2BE
在Rt△ADF中,∠FAD=60°
∴AD=![]() DF
DF
又∵AD=AC=AB
∴2BE=![]() DE,即
DE,即![]() BE=DF
BE=DF
∴![]() PB=PD
PB=PD

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目