题目内容
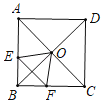
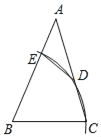
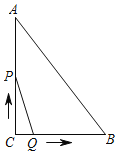
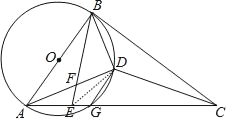
【题目】如图:AB是⊙O的直径,AC交⊙O于G,E是AG上一点,D为△BCE内心,BE交AD于F,且∠DBE=∠BAD.
(1)求证:BC是⊙O的切线;
(2)求证:DF=DG.
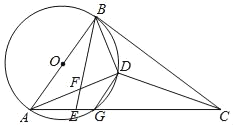
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)利用三角形内心性质得∠EBD=∠CBD.加上∠DBE=∠BAD,则∠CBD=∠BAD,根据圆周角定理得到∠BDA=90°.然后证明∠ABC=90°.于是根据切线的判定定理可判断BC是⊙O的切线;
(2)连接ED,如图,则∠BED=∠CED,再证明∠EFD=∠EGD,从而可判断△DFE≌△DGE.于是得到DF=DG.
(1)∵点D为△BCE的内心,
∴BD平分∠EBC.
∴∠EBD=∠CBD.
又∵∠DBE=∠BAD,
∴∠CBD=∠BAD.
又∵AB是圆的直径,
∴∠BDA=90°.
在Rt△BAD中,∠BAD+∠ABD=90°,
∴∠CBD+∠ABD=90°,即∠ABC=90°.
∴BC⊥AB.
又∵AB为直径,
∴BC是圆的切线;
(2)连接ED,如图,则ED平分∠BEC,
∴∠BED=∠CED.
∵∠EFD为△BFD的外角
∴∠EFD=∠ADB+∠EBD=90°+∠EBD,
又∵四边形ABDG为圆的内接四边形,
∴∠EGD=180°﹣∠ABD=180°﹣(90°﹣∠CDB)=90°+∠CDB
又∵∠EBD=∠CBD,
∴∠EFD=∠EGD
又∵ED=ED,
∴△DFE≌△DGE(AAS ).
∴DF=DG.

 阅读快车系列答案
阅读快车系列答案【题目】“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 | 清理养鱼网箱人数/人 | 清理捕鱼网箱人数/人 | 总支出/元 |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?