题目内容
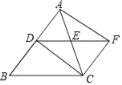
【题目】如图1,已知直角三角形ABC,∠ACB=90°,∠BAC=30°,点D是AC边上一点,过D作DE⊥AB于点E,连接BD,点F是BD中点,连接EF,CF.
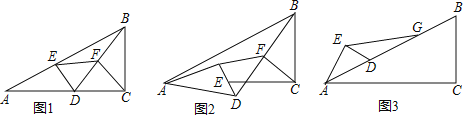
(1)发现问题:线段EF,CF之间的数量关系为_____;∠EFC的度数为_____;
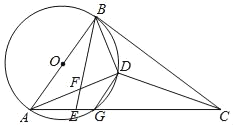
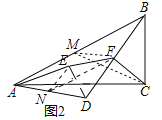
(2)拓展与探究:若将△AED绕点A按顺时针方向旋转α角(0°<α<30°),如图2所示,(1)中的结论还成立吗?请说明理由;
(3)拓展与运用:如图3所示,若△AED绕点A旋转的过程中,当点D落到AB边上时,AB边上另有一点G,AD=DG=GB,BC=3,连接EG,请直接写出EG的长度.
【答案】(1)EF=CF,120°;(2)结论成立,见解析;(3)EG=![]() .
.
【解析】
(1)利用直角三角形斜边中线定理及三角形外角性质解决问题即可;(2)结论成立.如图2中,取AB的中点M,AD的中点N,连接MC,MF,ED,EN,FN.想办法证明△MFC≌△NEF(SAS),可得结论;(3)如图3中,作EH⊥AB于H.想办法求出EH,HG即可解决问题.
(1)如图1中,
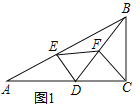
∵DE⊥AB,
∴∠BED=90°,
∵∠BCD=90°,BF=DF,∠A=30°,
∴FE=FB=FD=CF,∠ABC=60°,
∴∠FBE=∠FEB,∠FBC=∠FCB,
∴∠EFC=∠EFD+∠CFD=∠FBE+∠FEB+∠FBC+∠FCB=2(∠FBE+∠FBC)=2∠ABC=120°,
故答案为:EF=CF,120°.
(2)结论成立.
理由:如图2中,取AB的中点M,AD的中点N,连接MC,MF,ED,EN,FN.
∵BM=MA,BF=FD,
∴MF∥AD,MF=![]() AD,
AD,
∵AN=ND,
∴MF=AN,MF∥AN,
∴四边形MFNA是平行四边形,
∴NF=AM,∠FMA=∠ANF,
在Rt△ADE中,∵AN=ND,∠AED=90°,
∴EN=![]() AD=AN=ND,同理CM=
AD=AN=ND,同理CM=![]() AB=AM=MB,
AB=AM=MB,
在△AEN和△ACM中,
∠AEN=∠EAN,∠MCA=∠MAC,
∵∠MAC=∠EAN,
∴∠AMC=∠ANE,
又∵∠FMA=∠ANF,
∴∠ENF=∠FMC,
在△MFC和△NEF中,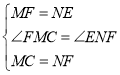 ,
,
∴△MFC≌△NEF(SAS),
∴FE=FC,∠NFE=∠MCF,
∵NF∥AB,
∴∠NFD=∠ABD,
∵∠ACB=90°,∠BAC=30°,
∴∠ABC=60°,△BMC是等边三角形,∠MCB=60°
∴∠EFC=∠EFN+∠NFD+∠DFC=∠MCF+∠ABD+∠FBC+∠FCB=∠ABC+∠MCB=60°+60°=120°.
(3)如图3中,作EH⊥AB于H.
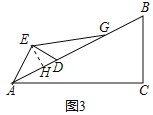
在Rt△ABC中,∵∠BAC=30°,BC=3,
∴AB=2BC=6,
在Rt△AED中,∠DAE=30°,AD=2,
∴DE=![]() AD=1,
AD=1,
在Rt△DEH中,∵∠EDH=60°,DE=1,
∴EH=EDsin60°=![]() ,
,
DH=EDcos60°=![]() ,
,
在Rt△EHG中,EG=![]() =
=![]() .
.