题目内容
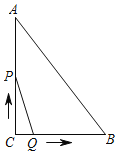
【题目】如图,在△ABC中,∠C=90°,AB=5cm,BC=3cm,动点P从点C出发,沿折线CA→AB以3cm/s的速度匀速运动,动点Q从C出发沿CB以1cm/s的速度匀速运动,若动点P、Q同时从点C出发任意一点到达B点时两点都停止运动,则这一过程中,△PCQ的面积S(cm2)与运动时间t(s)之间的关系大致图象是( )
A.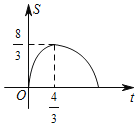 B.
B.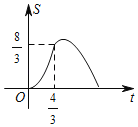
C.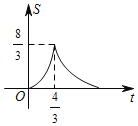 D.
D.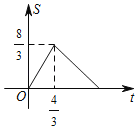
【答案】B
【解析】
当点P在AC段时,S=![]() ×PC×CQ=
×PC×CQ=![]() ×3t×t=
×3t×t=![]() t2,当点P在AB段时,S=
t2,当点P在AB段时,S=![]() ×CQ×PH=
×CQ×PH=![]() t×(9﹣3t)sinB=
t×(9﹣3t)sinB=![]() (﹣3t2+9t),即可求解.
(﹣3t2+9t),即可求解.
∵AB=5,BC=3,∠ACB=90°,
∴AC=4,AC+AB=9,
当点P在AC段时,S=![]() ×PC×CQ=
×PC×CQ=![]() ×3t×t=
×3t×t=![]() t2,为开口向上的抛物线,
t2,为开口向上的抛物线,
当点P在AB段时,过点P作PH⊥BC于点H,
S=![]() ×CQ×PH=
×CQ×PH=![]() t×(9﹣3t)sinB=
t×(9﹣3t)sinB=![]() (﹣3t2+9t),为开口向下的抛物线,
(﹣3t2+9t),为开口向下的抛物线,
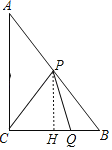
故选B.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目