题目内容
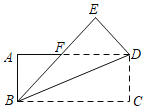
【题目】如图,在坡角为33°的山坡上有一建筑物AB,其正前方矗立着一大型广告牌,当阳光与水平线成45°角时,测得建筑物AB落在斜坡上的影子BD的长为6米,落在广告牌上的影子CD的长为4米,求建筑物AB的高(AB,CD均与水平面垂直,参考数据:sin33°=0.54,cos33°=0.84,tan33°=0.65)
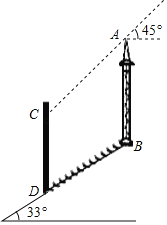
【答案】建筑物AB的高约为5.8m.
【解析】
过点C作CE⊥AB于E,过点B作BF⊥CD于F,根据正弦的定义求出DF,根据余弦的定义求出BF,根据矩形的性质、结合图形计算,得到答案.
解:过点C作CE⊥AB于E,过点B作BF⊥CD于F,
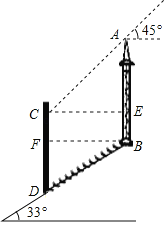
在Rt△BFD中,sin∠DBF=![]() ,
,
则DF=BDsin∠DBF≈6×0.54=3.24,
cos∠DBF=![]() ,
,
则BF=BDcos∠DBF≈6×0.84=5.04,
∵AB∥CD,CE⊥AB,BF⊥CD,
∴四边形BFCE为矩形,
∴BF=CE=5.04,CF=BE=CD﹣DF=4﹣3.24=0.76,
在Rt△ACE中,∠ACE=45°,
∴AE=CE=5.04,
∴AB=AE+BE=5.04+0.76=5.8,
答:建筑物AB的高约为5.8m.

练习册系列答案
相关题目