Question

【题目】取一副三角板按如图拼接，固定三角板ADC，将三角板ABC绕点A按顺时针方向旋转一个大小为的角()得三角形ABC′如图所示.

试问：(1)当旋转到如图的位置时，则= °；

(2)当= °时，能使如图中3的AB//CD；

(3)连接BD，当时，探寻∠DBC′+∠CAC′+∠BDC值的大小变化情况，并给出你的说明.

Answer 1

【答案】(1)45；(2)15；(3)∠DBC′+∠CAC′+∠BDC为定值105°，理由见解析.

【解析】

（1）当旋转到图2所示位置时，α=45°；
（2）若AB∥DC，则∠BAC=∠C=30°，得到α=∠BAC′-∠BAC=45°-30°=15°；
（3）连接CC′，BD，BO，在△BDO和△OCC′中，利用三角形内角和定理得到∠BDO+∠DBO=∠OCC′+∠OC′C，即可求得∠DBC′+∠CAC′+∠BDC=105°，即得到∠DBC′+∠CAC′+∠BDC值的大小不变．

解：（1）当旋转到图2所示位置时，
∵AB边旋转了45°，
∴α=45°，
故答案为：45；

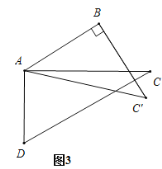
（2）如图3，
∵AB∥DC，
∴∠BAC=∠C=30°，
∴α=∠BAC′-∠BAC=45°-30°=15°，
所以当α=15°时，AB∥DC，
故答案为：15；

（3）当0°＜α≤45°时，∠DBC′+∠CAC′+∠BDC值的大小不变．

连接CC′，BD，BO，在△BDO和△OCC′中，∠BOD=∠COC′，
∴∠BDO+∠DBO=∠OCC′+∠OC′C，
∴∠DBC′+∠CAC′+∠BDC=∠BDO+∠α+∠DBO=∠OCC′+∠OC′C+∠α，
=180°-∠ACD-∠AC′B，
=180°-45°-30°
=105°，
∴当0°＜α≤45°时，∠DBC′+∠CAC′+∠BDC值的大小不变．