题目内容
【题目】如图,已知在Rt△ABC中,∠ABC=90°,AB=BC, BO是AC边上的中线,点P,D分别在AO和BC上,PB=PD,DE⊥AC于点E,


(1)求证:△BPO≌△PDE.
(2)若PB平分∠ABO,其余条件不变.求证:AP=CD.
(先将图形补充完整,然后再证明)
【答案】(1)证明见解析;(2)见解析.
【解析】分析:(1)根据等腰三角形的性质和三角形外角的性质可得到∠2=∠1+∠3=∠4+∠C,可得到∠3=∠4,可证明△BPO≌△PDE;(2)由角平分线的定义结合(1)可证得∠ABP=∠4,结合条件可证明△ABP≌△CPD,可证得AP=CD.
本题解析:
(1)证明:∵PB=PD,∴∠2=∠PBD,
∵AB=BC,∠ABC=90°,∴∠A=∠C =45°,
∵AB=BC, BO中线,∴BO⊥AC,∠1= ![]() =45°,∴∠1=∠C,
=45°,∴∠1=∠C,
∵∠PBC =∠3+∠1,∠2=∠4+∠C,∴∠3=∠4,
∵BO⊥AC,DE⊥AC,∴∠BOP=∠PED=90°,
在△BPO和△PDE中
∵∠3=∠4,∠BOP=∠PED, BP=PD
∴△BPO≌△PDE(AAS);
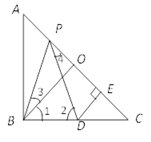
(2)证明:由(1)可得:∠3=∠4,
∵BP平分∠ABO,∴∠ABP=∠3,∴∠ABP=∠4,
在△ABP和△CPD中
∵∠A=∠C,∠ABP=∠4,PB=PD
∴△ABP≌△CPD(AAS)
∴AP=CD.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目