题目内容
【题目】如图,在平面直角坐标系中,矩形OABC的对角线OB、AC相交于点D,BE∥AC,AE∥OB.函数 ![]() (k>0,x>0)的图象经过点E.若点A、C的坐标分别为(3,0)、(0,2),则k的值为( )
(k>0,x>0)的图象经过点E.若点A、C的坐标分别为(3,0)、(0,2),则k的值为( )
A.3
B.4
C.4.5
D.6
【答案】C
【解析】解:∵BE∥AC,AE∥OB,
∴四边形AEBD是平行四边形,
∵四边形OABC是矩形,C的坐标为(0,2),
∴DA= ![]() AC,DB=
AC,DB= ![]() OB,AC=OB,AB=OC=2,
OB,AC=OB,AB=OC=2,
∴DA=DB,
∴四边形AEBD是菱形;
连接DE,交AB于F,如图所示:
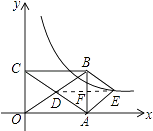
∵四边形AEBD是菱形,
∴AB与DE互相垂直平分,
∵OA=3,OC=2,
∴EF=DF= ![]() OA=
OA= ![]() ,AF=
,AF= ![]() AB=1,3+
AB=1,3+ ![]() =
= ![]() ,
,
∴点E坐标为:( ![]() ,1).
,1).
∵函数 ![]() (k>0,x>0)的图象经过点E,
(k>0,x>0)的图象经过点E,
∴k= ![]() ×1=
×1= ![]() .
.
所以答案是:C.
【考点精析】通过灵活运用矩形的性质,掌握矩形的四个角都是直角,矩形的对角线相等即可以解答此题.

练习册系列答案
相关题目