Question

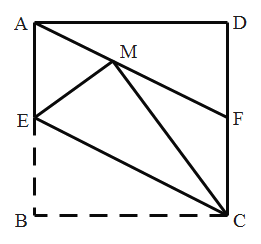
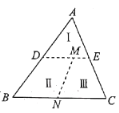
【题目】如图，现有一张三角形纸片，，，点，分别是，中点，点是上一定点，点是上一动点。将纸片依次沿，剪开，得到Ⅰ、Ⅱ和Ⅲ三部分，将Ⅱ绕点顺时针旋转，与重合，将Ⅲ绕点逆时针旋转，使与重合，拼成了一个新的图形，则这个新图形周长的最小值是（ ）

A.B.C.D.

Answer 1

【答案】C

【解析】

如图，作AJ⊥BC交DE于O，由题意旋转后的新图形是平行四边形GHPQ，周长=2DE+BC+2MN=16+2MN，当MN最小时，周长的值最小，根据垂线段最短求出MN的最小值即可解决问题．

解：如图，作AJ⊥BC交DE于O，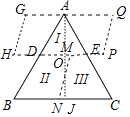

由题意旋转后的新图形是平行四边形GHPQ，周长=2DE+BC+2MN，
∵AD=DB，AE=EC，
∴DE∥BC，DE=BC=4，
∵S△ABC=BCAJ=28，
∴AJ=7，
∵AD=DB，DE∥BC，
∴AO=OJ=，
∴四边形GHPQ的周长=16+2MN，
∴当MN最小时，周长的值最小，根据垂线段最短可知MN的最小值为，
∴四边形GHPQ的周长的最小值为16+7=23，
故选：C．