题目内容
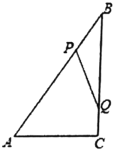
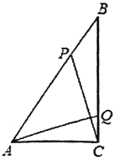
【题目】如图,直线![]() 与
与![]() 相离,过点
相离,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,![]() 交
交![]() 于点
于点![]() .点
.点![]() 在直线
在直线![]() 上,连接
上,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,在直线
,在直线![]() 上另取一点
上另取一点![]() ,使
,使![]() .
.

(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)已知![]() ,
,![]() ,
,![]() .
.
①求![]() 的半径
的半径![]() ;
;
②求![]() 的面积.
的面积.
【答案】(1)详见解析;(2)①![]() ;②
;②![]()
【解析】
(1)连接OD,知∠ABC=∠OBD=∠ODB,由∠PCD+∠ABC=90°知∠PCD+∠ODB=90°,结合∠PCD=∠PDC可得∠ODP=90°,即可得证;
(2)①由∠PCD=∠PDC知PC=PD=6、PA=5,根据PA2+AO2=PD2+OD2可得r=![]() ;②延长AO交⊙O于点F,连接DF,证△ABC∽△DBF得
;②延长AO交⊙O于点F,连接DF,证△ABC∽△DBF得![]() ,即可得DB的长,作DE⊥PC于点E,由△CAB∽△CED知
,即可得DB的长,作DE⊥PC于点E,由△CAB∽△CED知![]() ,求得DE,从而求得△PCD的面积.
,求得DE,从而求得△PCD的面积.
(1)证明:如图,连接![]() .
.
![]() .
.
![]() ,
,
![]() .
.
![]() .
.
![]() ,
,
![]() ,即
,即![]() .
.
![]() 是
是![]() 的切线.
的切线.
(2)解:①![]() ,
,
![]() .
.
![]() .
.
在![]() 和
和![]() 中,
中,
由![]() 可得
可得![]() ,
,
解得![]() .
.
②如图,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
![]() ,
,![]() ,
,
![]() .
.
![]() 即
即 .
.
![]() .
.
过点![]() 作
作![]() 于点
于点![]() ,
,
![]() .
.
![]() ,即
,即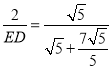 ,
,
解得![]() .
.
![]() .
.

 名校课堂系列答案
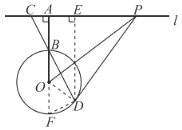
名校课堂系列答案【题目】为了解某校七年级学生的英语口语水平,随机抽取该年级部分学生进行英语口语测试,学生的测试成绩按标准定为A、B、C、D四个等级,并把测试成绩绘成如图所示的两个统计图表.
七年级英语口语测试成绩统计表
成绩 | 等级 | 人数 |
| A | 12 |
| B | m |
| C | n |
| D | 9 |
请根据所给信息,解答下列问题:
(1)本次被抽取参加英语口语测试的学生共有多少人?
(2)求扇形统计图中C级的圆心角度数;
(3)若该校七年级共有学生640人,根据抽样结课,估计英语口语达到B级以上![]() 包括B级
包括B级![]() 的学生人数.
的学生人数.
【题目】某篮球队对队员进行定点投篮测试,每人每天投篮10次,现对甲、乙两名队员在五天中进球数(单位:个)进行统计,结果如下:
甲 | 10 | 6 | 10 | 6 | 8 |
乙 | 7 | 9 | 7 | 8 | 9 |
经过计算,甲进球的平均数为8,方差为3.2.
(1)求乙进球的平均数和方差;
(2)如果综合考虑平均成绩和成绩稳定性两方面的因素,从甲、乙两名队员中选出一人去参加定点投篮比赛,应选谁?为什么?