题目内容
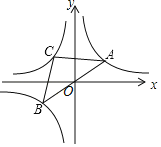
【题目】已知双曲线y=![]() 与直线y=x相交于AB两点,点C(2,2)、D(﹣2,﹣2)在直线上.
与直线y=x相交于AB两点,点C(2,2)、D(﹣2,﹣2)在直线上.
(1)若点P(1,m)为双曲线y=![]() 上一点,求PD﹣PC的值;
上一点,求PD﹣PC的值;
(2)若点P(x,y)(x>0)为双曲线上一动点,请问PD﹣PC的值是否为定值?请说明理由;
(3)若点P(x,y)(x>0)为双曲线上一动点,连接PC并延长PC交双曲线另一点E,当P点使得PD﹣CE=2PC时,求P的坐标.
【答案】(1)4;(2)PD﹣PC的值为定值4,理由见解析;(3)P(2+![]() ,2﹣
,2﹣![]() )或(2﹣
)或(2﹣![]() ,2+
,2+![]() ).
).
【解析】
(1)求出点P坐标,利用两点间距离公式计算即可.
(2)PD-PC的值为定值,理由为:把P坐标代入双曲线解析式表示出y,利用两点间的距离公式表示出PD与PC,求出之差即可.
(3)由题意PE=4.设直线PE的解析式为y=kx+b,由点C(2,2)在直线PE上可得b=2-2k,即得直线PE的解析式为y=kx+2-2k,则x1、x2是方程kx+2-2k=![]() 即kx2+(2-2k)x-2=0的两根,然后结合条件PE=4,运用两点间的距离公式和根与系数的关系求出k的值,代入方程kx2+(2-2k)x-2=0,解这个方程就可得到点P的坐标.
即kx2+(2-2k)x-2=0的两根,然后结合条件PE=4,运用两点间的距离公式和根与系数的关系求出k的值,代入方程kx2+(2-2k)x-2=0,解这个方程就可得到点P的坐标.
(1)∵点P(1,m)为双曲线y=![]() 上一点,
上一点,
∴m=2,
∴P(1,2),
∵C(2,2)、D(﹣2,﹣2),
∴PC=![]() =1,PD=
=1,PD=![]() =5,
=5,
∴PD=PC=5﹣1=4.
(2)PD﹣PC的值为定值4,理由为:
把P(x,y)代入双曲线解析式得:y=![]() ,即P(x,
,即P(x,![]() ),
),
∵C(2,2),D(﹣2,﹣2),x>0,
∴x+![]() ≥2
≥2 ![]() =2
=2![]() >2,
>2,
∴PD=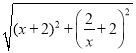 =
=![]() =
=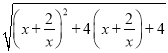 =x+
=x+![]() +2,
+2,
PC=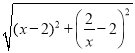 =
=![]() =
=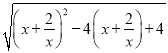 =x+
=x+![]() ﹣2,
﹣2,
则PD﹣PC=x+![]() +2﹣x﹣
+2﹣x﹣![]() +2=4;
+2=4;
(3)∵PD﹣CE=2PC,
∴PD﹣PC=PC+CE=4,
∴PE=4,
设直线PE的解析式为y=kx+b,
∵点C(2,2)在直线PE上,
∴2k+b=2,
∴b=2﹣2k,
∴直线PE的解析式为y=kx+2﹣2k,
设x1、x2是方程kx+2﹣2k=![]() 即kx2+(2﹣2k)x﹣2=0的两根,
即kx2+(2﹣2k)x﹣2=0的两根,
则有x1+x2=![]() =2﹣
=2﹣![]() ,x1x2=﹣
,x1x2=﹣![]() ,
,
∴(x1﹣x2)2=(x1+x2)2﹣4x1x2=(2﹣![]() )2﹣4(﹣
)2﹣4(﹣![]() )=4+
)=4+![]() ,
,
∴PE2=(x1﹣x2)2+(![]() ﹣
﹣![]() )2=(x1﹣x2)2+4
)2=(x1﹣x2)2+4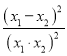 =(4+
=(4+![]() )+4
)+4![]() =4+
=4+![]() +4k2+4=
+4k2+4=![]() +4k2+8.
+4k2+8.
∵PE=4,
∴![]() +4k2+8=16,
+4k2+8=16,
∴![]() +4k2﹣8=0,
+4k2﹣8=0,
整理得(k2﹣1)2=0,
解得k1=1,k2=﹣1.
由条件“延长PC交双曲线另一点E”可得k<0,
∴k=﹣1,
代入kx2+(2﹣2k)x﹣2=0得,
﹣x2+4x﹣2=0,
解得x1=2+![]() ,x2=2﹣
,x2=2﹣![]() .
.
当x=2+![]() 时,P坐标为(2+
时,P坐标为(2+![]() ,2﹣
,2﹣![]() );当x=2﹣
);当x=2﹣![]() 时,P坐标为(2﹣
时,P坐标为(2﹣![]() ,2+
,2+![]() ).
).

 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案【题目】某农科所在相同条件下做某种作物种子发芽率的试验,结果如表所示:
种子个数n | 1000 | 1500 | 2500 | 4000 | 8000 | 15000 | 20000 | 30000 |
发芽种子个数m | 899 | 1365 | 2245 | 3644 | 7272 | 13680 | 18160 | 27300 |
发芽种子频率 | 0.899 | 0.910 | 0.898 | 0.911 | 0.909 | 0.912 | 0.908 | 0.910 |
则该作物种子发芽的概率约为_____________.(保留一位小数)