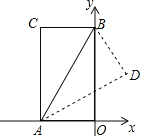
题目内容
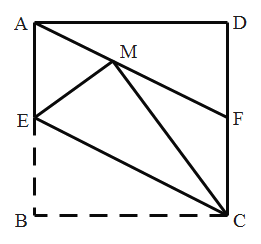
【题目】如图，在正方形
中，
是
边的中点，将
沿
折叠，使点
落在点
处，
的延长线与
边交于点
.下列四个结论:①
;②
;③
;④
S正方形ABCD，其中正确结论的个数为（ ）
A.
个B.
个C.
个D.
个
【答案】D
【解析】
根据折叠的性质，正方形的性质，等边对等角，同角的余角相等即可判断①；
根据题意先证明四边形AECF为平行四边形，再根据平行四边形的性质即可判断②；
过点E作
，根据三线合一及折叠的性质即可得出
，再根据同角的余切值相等得出比值，
，用a表示AM,MF的值，即可得出比值，判断③；
设，用a表示
及
的值，即可判断④.
E是AB的中点
AE=BE
沿
折叠
BE=EM,
故①正确；
四边形ABCD为正方形
沿折叠
四边形AECF为平行四边形
又E是AB的中点
故②正确；
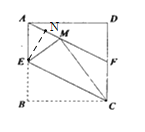
过点E作
由①知，
由②知，
E是AB的中点
设
则
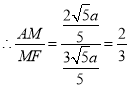
故③正确；
设
则
，
，
，
，
故④正确.
故选D.
练习册系列答案
手拉手全优练考卷系列答案
相关题目
【题目】某农科所在相同条件下做某种作物种子发芽率的试验，结果如表所示：
种子个数n | 1000 | 1500 | 2500 | 4000 | 8000 | 15000 | 20000 | 30000 |
发芽种子个数m | 899 | 1365 | 2245 | 3644 | 7272 | 13680 | 18160 | 27300 |
发芽种子频率 | 0.899 | 0.910 | 0.898 | 0.911 | 0.909 | 0.912 | 0.908 | 0.910 |
则该作物种子发芽的概率约为_____________．（保留一位小数）
