题目内容
【题目】根据要求解方程
（1）x2+3x﹣4＝0（公式法）；
（2）x2+4x﹣12＝0（配方法）；
（3）（x+4）2＝7（x+4）（适当的方法）．
【答案】(1) x1＝﹣4，x2＝1；(2) x1＝﹣6，x2＝2；(3) x1＝3，x2＝﹣4
【解析】
（1）直接求出△=b2-4ac=25，进而利用公式法解方程即可；
（2）直接利用配方法解方程得出答案；
（3）直接利用提取公因式法解方程得出答案．
（1）∵△=b2-4ac=25＞0，
∴x=
，
解得：x1=-4，x2=1；
（2）x2+4x-12=0，
x2+4x=12，
（x+2）2=16，
则x+2=±4，
解得：x1=-6，x2=2；
（3）（x+4）2=7（x+4）
（x+4）[（x+4）-7]=0，
则x+4=0或x-3=0，
解得：x1=3，x2=-4．
阅读快车系列答案
【题目】某校在七年级、八年级开展了阅读文学名著知识竞赛．该校七、八年级各有学生400人，各随机抽取20名学生进行了抽样调查，获得了他们知识竞赛成绩（单位：分），并对数据进行整理、描述和分析．下面给出了部分信息．
a．七年级学生知识竞赛成绩的平均数、中位数、众数、优秀率（80分及以上）如下表所示：
年级 | 平均数 | 中位数 | 众数 | 优秀率 |
七年级 | 84. 2 | 77 | 74 | 45﹪ |
b．八年级学生知识竞赛成绩的扇形统计图如下（数据分为5组，A：50≤x≤59； B：60≤x≤69；C：70≤x≤79；D：80≤x≤89；E：90≤x≤100）
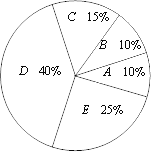
c．八年级学生知识竞赛成绩在D组的是：87 88 88 88 89 89 89 89
根据以上信息，回答下列问题：
（1）八年级学生知识竞赛成绩的中位数是 分；
（2）请你估计该校七、八年级所有学生中达到“优秀”的有多少人？
（3）下列结论：①八年级成绩的众数是89分；②八年级成绩的平均数可能为86分；③八年级成绩的极差可能为50分．其中所有正确结论的序号是 ．