题目内容
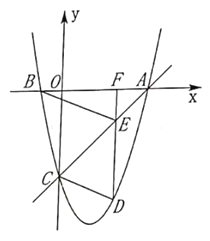
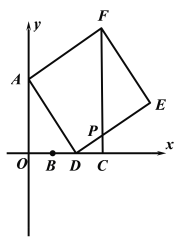
【题目】如图,在平面直角坐标系中,已知![]() ,
,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上的动点,以
上的动点,以![]() 为边向右侧作正方形
为边向右侧作正方形![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,则
,则![]() 的最大值______.
的最大值______.
【答案】![]()
【解析】
作FQ⊥y轴于点Q,证△AFQ≌△DAO得FQ=OA=6,求出FQ=OC,结合FQ∥OC且∠FQO=90°证四边形OCFQ是矩形,从而得∠PCD=∠AOD=90°,设OD=x,则CD=6-x(2≤x≤6),再证△AOD∽△DCP得![]() ,即则
,即则![]() ,即PC=-
,即PC=-![]() x2+x=-
x2+x=-![]() (x-3)2+
(x-3)2+![]() ,据此可得答案.
,据此可得答案.
解:如图,作FQ⊥y轴于点Q,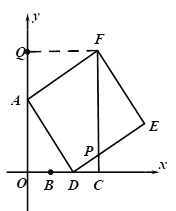
∵FQ⊥y
∴在Rt△AFQ中,∠FAQ+∠AFQ=90°,∠FQA=90°
∵四边形ADEF是正方形,
∴FA=AD,∠FAD=90°,
∴∠FAQ+∠DAO=90°,
∴∠AFQ=∠DAO,
∵∠AOD=90°
∴∠FQA=∠AOD
在△AFQ和△DAO中,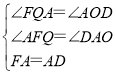
∴△AFQ≌△DAO(AAS),
∴FQ=OA=6,
∵![]()
∴FQ=OC
又∵∠FQA=∠AOD
∴FQ∥OC,
∴四边形OCFQ是平行四边形
∵∠FQO=90°,
∴四边形OCFQ是矩形,
∴∠PCD=∠AOD=90°
∴∠PDC+∠CPD=90°,
∵∠ADE=90°
∴∠ADO+∠PDC=90°,
∴∠CPD=∠ADO
∴△AOD∽△DCP,
∴![]() ,
,
设OD=x,则CD=6-x (2≤x≤6),
则![]() ,
,
即PC=-![]() x2+x=-
x2+x=-![]() (x-3)2+
(x-3)2+![]() ,
,
∴当x=3时,PC最大=![]() ,
,
故答案为:![]() .
.

【题目】某农科所在相同条件下做某种作物种子发芽率的试验,结果如表所示:
种子个数n | 1000 | 1500 | 2500 | 4000 | 8000 | 15000 | 20000 | 30000 |
发芽种子个数m | 899 | 1365 | 2245 | 3644 | 7272 | 13680 | 18160 | 27300 |
发芽种子频率 | 0.899 | 0.910 | 0.898 | 0.911 | 0.909 | 0.912 | 0.908 | 0.910 |
则该作物种子发芽的概率约为_____________.(保留一位小数)