题目内容
【题目】如图，已知抛物线y=ax2+bx+c（a≠0）交x轴于A（﹣1，0），B（5，0）两点，与y轴交于点C（0，2）
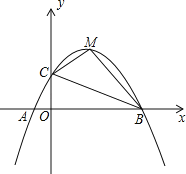
（1）求抛物线的解析式；
（2）若点M为抛物线的顶点，连接BC、CM、BM，求△BCM的面积；
（3）连接AC，在x轴上是否存在点P使△ACP为等腰三角形？若存在，请求出点P的坐标；若不存在，请说明理由．
【答案】（1）y=﹣
x2+
x+2；（2）6；（3）存在P1、P2、P3、P4四个点，它们的坐标分别是P1（﹣1﹣
，0）、P2（﹣1，0）、P3（
，0）、P4（1，0）．
【解析】
试题分析：(1)、将A（﹣1，0），B（5，0），C（0，2）三点坐标分别代入y=ax2+bx+c，求出a、b、c的值，从而确定抛物线解析式；(2)、先求出顶点M的坐标，然后过M作MN垂直y轴于N，把△BCM的面积转化成梯形OBMN的面积减去两个直角三角形的面积,求出相应的长度，代入面积公式即可；(3)、因为P点在x轴上，∴P点纵坐标为0，因为AO=1，CO=2，所以AC=，然后分类讨论，根据AC为腰，AC为底两种情况求P点坐标．当AC为腰时，分为A为等腰三角形的顶点（左右各有一点P），C为等腰三角形的顶点（有一点P），两种情况求P点坐标；当AC为底，P为顶点时，作线段AC的垂直平分线交x轴于点P，利用勾股定理求出OP,进而得到P点坐标．
试题解析：(1)、因为抛物线经过A,B,C三点，所以将A（﹣1，0），B（5，0），C（0，2）分别代入y=ax2+bx+c得，a-b+c=0,25a+5b+c=0,c=2；组成三元一次方程组，解得a=﹣
,b=,c=2,∴抛物线的解析式是y=﹣x2+x+2；
(2)、先根据顶点坐标公式：
，和解析式求出顶点M的坐标，顶点M的坐标是M（2，
）．
过M作MN垂直y轴于N，如图，S△BCM=S四边形OBMN﹣S△OBC﹣S△MNC，其中CN=-2=,MN=2，BO=5，∴S△BCM=
（2+5）﹣×5×2﹣×（﹣2）×2=6；
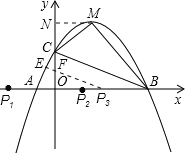
(3)、因为P点在x轴上，∴P点纵坐标为0，因为AO=1，CO=2，所以AC=
，分类讨论，根据AC为腰，AC为底两种情况求P点坐标．当以AC为腰时，在x轴上有两个点分别为P1，P2，AP1=AP2=AC=,P1在x轴负半轴，P2在x轴正半轴，∵0P1=1+，OP2=﹣1，∴P1，P2的坐标分别是P1（﹣1﹣，0），P2（﹣1，0）；当以AC为底,P为顶点时，作AC的垂直平分线交x轴于P3，连接CP3,设OP3为x，因为CP3=AP3，由勾股定理得：
，解得x=
,则P3的坐标为P3（，0）．当AC为腰， C为等腰三角形的顶点时，AC=PC，OP=AO=1,则P4（1，0）．所以存在P1、P2、P3、P4四个点，使△ACP为等腰三角形,它们的坐标分别是P1（﹣1﹣，0）、P2（﹣1，0）、P3（，0）、P4（1，0）．
