题目内容
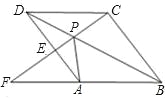
【题目】如图,在△ABD和△ACE中,有下列判断:
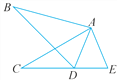
①AB=AC;②∠B=∠C;③∠BAC=∠EAD;④AD=AE.
请用其中的三个判断作为条件,余下的一个判断作为结论(用序号的形式),写出一个由三个条件能推出结论成立的式子,并说明理由.
【答案】证明见解析
【解析】试题分析:
按题中要求,选3个作条件,1个作结论,则有:(1)① ② ③ ④ ;(2)①②④③;(3)①③④②;(4)②③④①;共计四种组合方式.然后根据全等三角形的判定方法,可知其中(2)不能判定△ABD≌△ACE,从而不能得到结论,其余的三种组合都可以通过证△ABD≌△ACE而得到结论,故有三种组合方式是成立的,我们选择其中一个进行证明即可.
试题解析:
(1)有三种组合是成立的:① ② ③④ 或①③④② 或②③④①.
(2)如①②③④ 理由如下:
∵∠BAC=∠EAD,
∴∠BAC+∠CAD=∠EAD+∠CAD,即∠BAD=∠CAE,
∴在△ABD和△ACE中: 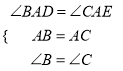 ,
,
∴△ABD≌△ACE(ASA).
∴ AD=AE.

练习册系列答案
相关题目