题目内容
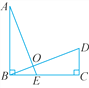
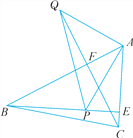
【题目】如图,已知在△ABC中,AB>AC,BE,CF都是△ABC的高线,P是BE上一点,且BP=AC,Q是CF延长线上一点,且CQ=AB,连结AP,AQ,QP.求证:
(1)AQ=PA.
(2)AP⊥AQ.
【答案】(1)证明见解析(2)证明见解析
【解析】试题分析:(1)由已知条件可求出∠ABP=∠QCA,即可根据SAS证得△AQC≌△PAB(SAS),就可以得出AP=AQ;
(2)根据全等三角形的性质,由△AQC≌△PAB可得出∠BAP=∠CQA,再由∠CQA+∠FAQ=90°,即可证明.
试题解析:(1)∵BE,CF是△ABC的高线,
∴BE⊥AC,CF⊥AB,
∴∠ABP+∠BAC=∠ACQ+∠BAC=90°,
∴∠ABP=∠ACQ.
在△AQC和△PAB中,∵ 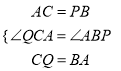
∴△AQC≌△PAB(SAS).∴AQ=PA.
(2)∵△AQC≌△PAB,∴∠BAP=∠CQA.
∵∠CQA+∠BAQ=90°,
∴∠BAP+∠BAQ=90°,∴AP⊥AQ.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目