题目内容
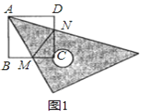
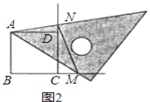
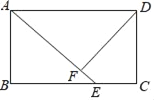
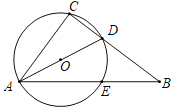
【题目】如图,Rt△ABC中,∠C=90°,AB=4![]() ,在BC上取一点D,连结AD,作△ACD的外接圆⊙O,交AB于点E.张老师要求添加条件后,编制一道题目,并解答.
,在BC上取一点D,连结AD,作△ACD的外接圆⊙O,交AB于点E.张老师要求添加条件后,编制一道题目,并解答.
(1)小明编制题目是:若AD=BD,求证:AE=BE.请你解答.
(2)在小明添加条件的基础上请你再添加一条线段的长度,编制一个计算题(不标注新的字母),并直接给出答案.(根据编出的问题层次,给不同的得分)
【答案】(1)见解析;(2)若CD=3,AC=4
【解析】
(1)连结DE,由题可推出DE⊥AB,再根据AD=BD,利用等腰三角形三线合一的性质即可证明;
(2)此题答案不唯一,根据现有条件添加一条线段的长度提出一个问题,解答即可.
(1)证明:连结DE,
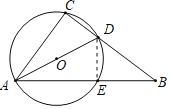
∵∠C=90°,
∴AD为直径,
∴DE⊥AB,
∵AD=BD,
∴AE=BE;
(2)若CD=3,求AC的长,
设BD=x,
∵∠B=∠B,∠C=∠DEB=90°,
∴△ABC~△DBE,
∴![]() ,
,
∴![]() ,
,
∴x=5,
∴AD=BD=5,
∴AC=![]() =4.
=4.

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案【题目】2020年4月是我国第32个爱国卫生月.某校九年级通过网课举行了主题为“防疫有我,爱卫同行”的知识竞赛活动.为了解全年级500名学生此次竞赛成绩(百分制)的情况,随机抽取了部分参赛学生的成绩,整理并绘制出如下不完整的统计表(表1)和统计图(如图).请根据图表信息解答以下问题:
(1)本次调查一共随机抽取了____个参赛学生的成绩;
(2)表1中a=__;
(3)所抽取的参赛学生的成绩的中位数落在的“组别”是__;
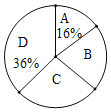
(4)统计图中B组所占的百分比是_______;
(5)请你估计,该校九年级竞赛成绩达到80分以上(含80分)的学生人数.
表1 知识竞赛成绩分组统计表
组别 | 分数/分 | 频数 |
A | 60≤x<70 | a |
B | 70≤x<80 | 10 |
C | 80≤x<90 | 14 |
D | 90≤x<100 | 18 |