题目内容
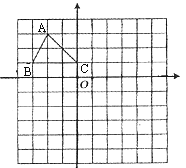
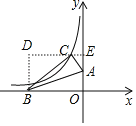
【题目】如图,已知点A(0,1),B(﹣3,0),连接AB,将△ABO沿AB翻折,使点O与点C重合,且点C恰好在函数y=![]() 上,则k的值为( )
上,则k的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
过C点作CE⊥y轴于E,作BD⊥CE于D,如图,设AE=m,CE=n,先根据折叠的性质得BC=BO=3,AC=OA=1,∠ACB=∠AOB=90°,再证明Rt△ACE∽Rt△CBD,利用相似比得到CD=3m,BD=3n,则3n=m+1,3m+n=3,于是可求出得m=![]() ,n=
,n=![]() ,从而得到C点坐标,然后利用反比例函数图象上点的坐标特征求出k的值.
,从而得到C点坐标,然后利用反比例函数图象上点的坐标特征求出k的值.
解:过C点作CE⊥y轴于E,作BD⊥CE于D,如图,设AE=m,CE=n,
∵点A(0,1),B(﹣3,0),
∴OB=3,OA=1,
∵△ABO沿AB翻折,使点O与点C重合,
∴BC=BO=3,AC=OA=1,∠ACB=∠AOB=90°,
∵∠ACE+∠BCD=90°,∠ACE+∠CAE=90°,
∴∠BCD=∠CAE,
∴Rt△ACE∽Rt△CBD,
∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,
,
∴CD=3m,BD=3n,
∴3n=m+1,3m+n=3,解得m=![]() ,n=
,n=![]() ,
,
∴OE=1+![]() =
=![]() ,
,
∴C点坐标为(﹣![]() ,
,![]() ),
),
∵点C好在函数y=![]() 上,
上,
∴k=﹣![]() ×
×![]() =﹣
=﹣![]() .
.
故选:B.

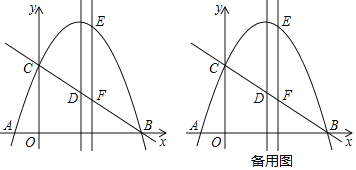
【题目】如图,点P是![]() 上一动点,连接AP,作∠APC=45°,交弦AB于点C.AB=6cm.
上一动点,连接AP,作∠APC=45°,交弦AB于点C.AB=6cm.

小元根据学习函数的经验,分别对线段AP,PC,AC的长度进行了测量.
下面是小元的探究过程,请补充完整:
(1)下表是点P是![]() 上的不同位置,画图、测量,得到线段AP,PC,AC长度的几组值,如下表:
上的不同位置,画图、测量,得到线段AP,PC,AC长度的几组值,如下表:
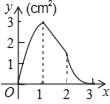
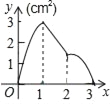
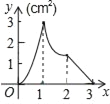
AP/cm | 0 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
PC/cm | 0 | 1.21 | 2.09 | 2.69 | m | 2.82 | 0 |
AC/cm | 0 | 0.87 | 1.57 | 2.20 | 2.83 | 3.61 | 6.00 |
①经测量m的值是 (保留一位小数).
②在AP,PC,AC的长度这三个量中,确定![]() 的长度是自变量,
的长度是自变量,![]() 的长度和 的长度都是这个自变量的函数;
的长度和 的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数图象;

(3)结合函数图象,解决问题:当△ACP为等腰三角形时,AP的长度约为 cm(保留一位小数).