Question

【题目】小王电子产品专柜以20元/副的价格批发了某新款耳机，在试销的60天内整理出了销售数据如下

销售数据(第x天)	售价(元)	日销售量(副)
1≤x＜35	x+30	100﹣2x
35≤x≤60	70	100﹣2x

(1)若试销阶段每天的利润为W元，求出W与x的函数关系式；

(2)请问在试销阶段的哪一天销售利润W可以达到最大值？最大值为多少？

Answer 1

【答案】(1)见解析；(2)在试销阶段的第20天时W最大，最大值为1800元．

【解析】

（1）利用总利润＝单件利润×销量写出函数关系式即可；

（2）配方后确定两个最值，取最大的即可．

解：(1)①当1≤x＜35时，W1＝(x+30﹣20)(100﹣2x)

即W1＝﹣2(x﹣20)2+1800；

②当35≤2x≤26时，W2＝(70﹣20)(100﹣2x)

即W2＝﹣100x+5000；

故W与x之间的函数关系式为：

W＝；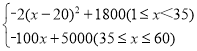

(2)∵W1＝﹣2(x﹣20)2+1800(1≤x＜35)，

∴在试销的第一阶段，在第20天时，利润最大为1800元，

∵W2＝﹣100x+5000(35≤x≤60)，

∴在试销的第二阶段，在第35天时，销售利润最大为1500元，

答：在试销阶段的第20天时W最大，最大值为1800元．