题目内容
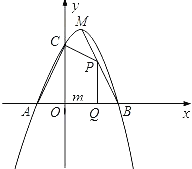
【题目】如图,在平面直角坐标系中,抛物线![]() 的图象经过
的图象经过![]() 和
和![]() 两点,且与
两点,且与![]() 轴交于
轴交于![]() ,直线
,直线![]() 是抛物线的对称轴,过点
是抛物线的对称轴,过点![]() 的直线
的直线![]() 与直线相交于点
与直线相交于点![]() ,且点
,且点![]() 在第一象限.
在第一象限.

(1)求该抛物线的解析式;
(2)若直线![]() 和直线
和直线![]() 、
、![]() 轴围成的三角形面积为6,求此直线的解析式;
轴围成的三角形面积为6,求此直线的解析式;
(3)点![]() 在抛物线的对称轴上,
在抛物线的对称轴上,![]() 与直线
与直线![]() 和
和![]() 轴都相切,求点
轴都相切,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)根据图象经过M(1,0)和N(3,0)两点,且与y轴交于D(0,3),可利用待定系数法求出二次函数解析式;
(2)根据直线AB与抛物线的对称轴和x轴围成的三角形面积为6,得出AC,BC的长,得出B点的坐标,即可利用待定系数法求出一次函数解析式;
(3)利用三角形相似求出△ABC∽△PBF,即可求出圆的半径,即可得出P点的坐标.
(1)![]() 抛物线
抛物线![]() 的图象经过
的图象经过![]() ,
,![]() ,
,![]() ,
,
![]() 把
把![]() ,
,![]() ,
,![]() 代入得:
代入得:
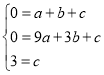
解得: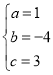 ,
,
![]() 抛物线解析式为
抛物线解析式为![]() ;
;
(2)![]() 抛物线
抛物线![]() 改写成顶点式为
改写成顶点式为![]() ,
,
![]() 抛物线对称轴为直线
抛物线对称轴为直线![]() ,
,
∴对称轴与![]() 轴的交点C的坐标为
轴的交点C的坐标为![]()
![]() ,
,
![]() ,
,
设点B的坐标为![]() ,
,![]() ,
,
则![]() ,
,
![]() ,
,
∴![]()
∴点B的坐标为![]() ,
,
设直线![]() 解析式为:
解析式为:![]() ,
,
把![]() ,
,![]() 代入得:
代入得:![]() ,
,
解得:![]() ,
,
![]() 直线
直线![]() 解析式为:
解析式为:![]() .
.
(3)①∵当点P在抛物线的对称轴上,⊙P与直线AB和x轴都相切,
设⊙P与AB相切于点F,与x轴相切于点C,如图1;
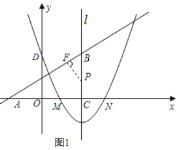
∴PF⊥AB,AF=AC,PF=PC,
∵AC=1+2=3,BC=4,
∴AB=![]() =5,AF=3,
=5,AF=3,
∴BF=2,
∵∠FBP=∠CBA,
∠BFP=∠BCA=90![]() ,
,
∴△ABC∽△PBF,
∴![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴点P的坐标为(2,![]() );
);
②设⊙P与AB相切于点F,与![]() 轴相切于点C,如图2:
轴相切于点C,如图2:
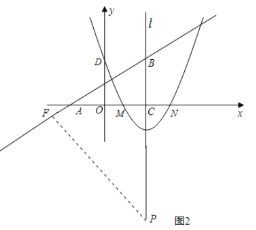
∴PF⊥AB,PF=PC,
∵AC=3,BC=4, AB=5,
∵∠FBP=∠CBA,
∠BFP=∠BCA=90![]() ,
,
∴△ABC∽△PBF,
∴![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴点P的坐标为(2,-6),
综上所述,![]() 与直线
与直线![]() 和
和![]() 都相切时,
都相切时,
![]() 或
或![]() .
.