题目内容
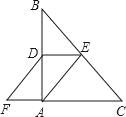
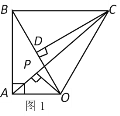
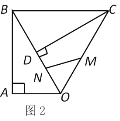
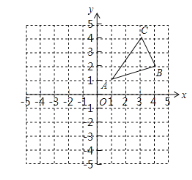
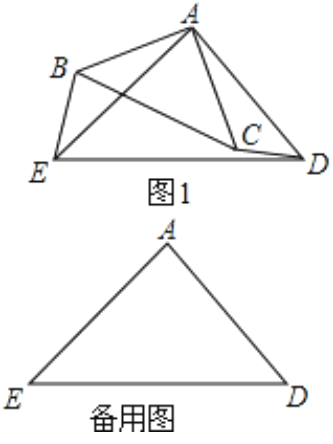
【题目】如图1,△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,点B在线段AE上,点C在线段AD上,如图2,△ABC以点A为旋转中心顺时针旋转.
(1)证明:BE=CD
(2)当AC=![]() ED时,探究在△ABC旋转的过程中,是否存在这样的旋转角α,使以A、B、C、D四点为顶点的四边形是平行四边形?若存在,求出角α的度数;若不存在,请说明理由.
ED时,探究在△ABC旋转的过程中,是否存在这样的旋转角α,使以A、B、C、D四点为顶点的四边形是平行四边形?若存在,求出角α的度数;若不存在,请说明理由.
【答案】(1)见解析;(2)存在,角α=![]() 或
或![]() 或
或![]() .
.
【解析】
(1)根据等腰直角三角形的性质可得![]() ,
,![]() ,由
,由![]() ,根据等式的性质可得
,根据等式的性质可得![]() ,根据SAS可证
,根据SAS可证![]() ≌
≌![]() ,根据全等三角形的性质即可求解;
,根据全等三角形的性质即可求解;
(2)先由AC=![]() ED,设
ED,设![]() ,
,![]() ,取ED的中点H,把各条线段表示出来,再以从一个顶点发出的线段
,取ED的中点H,把各条线段表示出来,再以从一个顶点发出的线段![]() 是否对角线来不重不漏地讨论,前两种情况已经有一组对边相等,只需这组对边平行即可,由平行线的判定,可知只需内错角相等即可,继而得到相应的旋转角度,第3种情况,因为没有判定平行四边形的现成条件,就先假设是平行四边形,在此基础上推得旋转角度,再论证以这个旋转角度为前提的四边形是平行四边形.
是否对角线来不重不漏地讨论,前两种情况已经有一组对边相等,只需这组对边平行即可,由平行线的判定,可知只需内错角相等即可,继而得到相应的旋转角度,第3种情况,因为没有判定平行四边形的现成条件,就先假设是平行四边形,在此基础上推得旋转角度,再论证以这个旋转角度为前提的四边形是平行四边形.
解:(1)![]() 和
和![]() 都是等腰直角三角形,
都是等腰直角三角形,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵在![]() 与
与![]() 中,
中,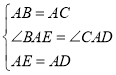 ,
,![]() ≌
≌![]()
![]() ;
;
(2)∵AC=![]() ED,设
ED,设![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
取ED的中点H,则![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
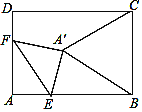
①若![]() 是四边形的对角线,如下图中的四边形
是四边形的对角线,如下图中的四边形![]() ,
,
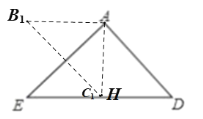
要使得四边形![]() 是平行四边形,已有
是平行四边形,已有![]() ,只需
,只需![]() ,
,
只需![]() ,
,
②若![]() 是四边形的对角线,如下图中的四边形
是四边形的对角线,如下图中的四边形![]() ,
,
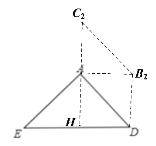
同理只需![]() ,
,
∴![]() ;
;
③若![]() 是四边形的对角线,如下图中的四边形
是四边形的对角线,如下图中的四边形![]() ,
,
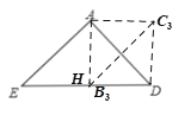
若四边形![]() 是平行四边形,
是平行四边形,
又∵![]() ,
,![]() ,
,
∴四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() ,
,
又因为![]() ,
,![]() ,
,
∴![]() 重合,
重合,
此时![]() ,
,![]()
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]()
∴四边形![]() 是平行四边形;
是平行四边形;
综上所述:角![]() 的度数是
的度数是![]() 或
或![]() 或
或![]() .
.

练习册系列答案
相关题目