题目内容
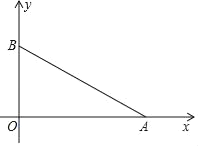
【题目】已知![]() 中,
中,![]() ,
,![]() ,
,![]() .将
.将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 后得到
后得到![]() ,其中点
,其中点![]() 运动的路径为
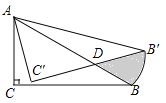
运动的路径为![]() .那么图中阴影部分的面积是____.
.那么图中阴影部分的面积是____.
【答案】![]()
【解析】
根据直角三角形的性质得到∠CAB=60![]() ,AB=2AC=2,求得BC=
,AB=2AC=2,求得BC=![]() ,根据旋转的性质得到AC′=AC=1,AB′=AB=2,B′C′=BC=
,根据旋转的性质得到AC′=AC=1,AB′=AB=2,B′C′=BC=![]() ,∠B′AB=30
,∠B′AB=30![]() ,∠C′AB′=∠CAB=60
,∠C′AB′=∠CAB=60![]() ,在Rt△AC′D中求得C′D=AC′=1,根据三角形和扇形的面积公式即可得到结论.
,在Rt△AC′D中求得C′D=AC′=1,根据三角形和扇形的面积公式即可得到结论.
∵∠C=90![]() ,∠ABC=30
,∠ABC=30![]() ,AC=1
,AC=1
∴∠CAB=60![]() ,AB=2AC=2,
,AB=2AC=2,
∴BC=![]() ,
,
∵Rt△ABC绕点A逆时针旋转15![]() 后得到△AB′C′,
后得到△AB′C′,
∴AC′=AC=1,AB′=AB=2,B′C′=BC=![]() ,∠B′AB=15
,∠B′AB=15![]() ,∠C′AB′=∠CAB=60
,∠C′AB′=∠CAB=60![]() ,
,
∴∠C′AD=∠C′AB′-∠BAB′=45![]() ,
,
在Rt△AC′D中,∵∠C′AD=45![]() ,
,
∴C′D=AC′=1,
∴B′D=B′C′C′D=![]() 1,
1,
∴图中阴影部分的面积=S扇形BAB′S△ADB′
=![]()
=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目
【题目】为支持国家南水北调工程建设,小王家由原来养殖户变为种植户,经市场调查得知,当种植樱桃的面积x不超过15亩时,每亩可获得利润y=1900元;超过15亩时,每亩获得利润y(元)与种植面积x(亩)之间的函数关系如下表(为所学过的一次函数,反比例函数或二次函数中的一种)
x(亩) | 20 | 25 | 30 | 35 |
y(元) | 1800 | 1700 | 1600 | 1500 |
(1)请求出种植樱桃的面积超过15亩时每亩获得利润y与x的函数关系式;
(2)如果小王家计划承包荒山种植樱桃,受条件限制种植樱桃面积x不超过50亩,设小王家种植x亩樱桃所获得的总利润为W元,求小王家承包多少亩荒山获得的总利润最大,并求总利润W(元)的最大值.