Question

【题目】如图，将矩形ABCD的四个角向内折起，恰好拼成一个既无缝隙又不重叠的四边形EFGH，若EH＝4，EF＝5，那么线段AD与AB的比等于_____．

Answer 1

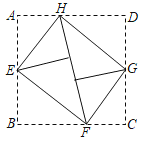
【答案】．

【解析】

先根据图形翻折的性质可得到四边形EFGH是矩形，由“AAS”可证Rt△AHE≌Rt△CFG，可得AH=CF=FN，再由勾股定理及直角三角形的面积公式求出AD，AB的长，即可求解．

如图：

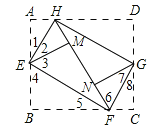
由折叠的性质可得：∠1＝∠2，∠3＝∠4，AE＝EM＝BE，DH＝HN，CF＝FN，

∴∠2+∠3＝90°，

∴∠HEF＝90°，

同理四边形EFGH的其它内角都是90°，

∴四边形EFGH是矩形．

∴EH＝FG；

又∵∠1+∠4＝90°，∠4+∠5＝90°，

∴∠1＝∠5，

同理∠5＝∠7＝∠8，

∴∠1＝∠8，

∴Rt△AHE≌Rt△CFG（AAS），

∴AH＝CF＝FN，

又∵HD＝HN，

∴AD＝HF，

在Rt△HEF中，EH＝4，EF＝5，根据勾股定理得HF＝＝＝AD，

∵S△EFH＝×EF×EH＝×HF×EM，

∴EM＝，

∴AB＝2AE＝2EM＝，

∴AD：AB＝41：40＝，

故答案为：．