题目内容
在平面直角坐标系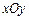 中,矩形ABCO的面
中,矩形ABCO的面 积为15,边OA比OC大2,E为BC的中点,以OE为直径的⊙O′交x轴于D点,过点D作DF⊥AE于F.
积为15,边OA比OC大2,E为BC的中点,以OE为直径的⊙O′交x轴于D点,过点D作DF⊥AE于F.
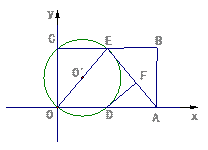
(1) 求OA,OC的长;
(2) 求证:DF为⊙O′的切线;
(3)由已知可得,△AOE是等腰三角形.那么在直线BC上是否存在除点E以外的点P,使△AOP也是等腰三角形?如果存在,请你证明点P与⊙O′的位置关系,如果不存在,请说明理由.
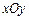 中,矩形ABCO的面
中,矩形ABCO的面 积为15,边OA比OC大2,E为BC的中点,以OE为直径的⊙O′交x轴于D点,过点D作DF⊥AE于F.
积为15,边OA比OC大2,E为BC的中点,以OE为直径的⊙O′交x轴于D点,过点D作DF⊥AE于F. 
(1) 求OA,OC的长;
(2) 求证:DF为⊙O′的切线;
(3)由已知可得,△AOE是等腰三角形.那么在直线BC上是否存在除点E以外的点P,使△AOP也是等腰三角形?如果存在,请你证明点P与⊙O′的位置关系,如果不存在,请说明理由.
(1)解:在矩形ABCO中,设OC=x,则OA=x+2,
依题意得,x(x+2)=15.
解得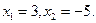 (不合题意,舍去)
(不合题意,舍去)
∴ OC="3" ,OA="5" . …………………………………1分
(2)证明:连结O′D,在矩形OABC中,
∵ OC=AB,∠OCB=∠ABC,E为BC的中点,
∴△OCE≌△ABE .
∴ EO="EA" .
∴∠EOA=∠EAO .
又∵O′O= O′D,
∴ ∠O′DO=∠EOA=∠EAO.
∴ O′D∥EA .
∵ DF⊥AE,
∴ DF⊥O′D .
又∵点D在⊙O′上,O′D为⊙O′的半径,
∴ DF为⊙O′的切线. …………………………………3分
(3)答:存在 .
当OA=AP时,以点A为圆心,以AO为半径画弧,交BC于点 和
和 两点,
两点,
则△AO 、△AO
、△AO 均为等腰三角形.
均为等腰三角形.
证明:过 点作
点作 H⊥OA于点H,则
H⊥OA于点H,则 H=OC=3,
H=OC=3,
∵ A =OA=5,
=OA=5,
∴ AH=4,OH=1.
∴ (1,3).
(1,3).
∵ (1,3)在⊙O′的弦CE上,且不与C、E重合,
(1,3)在⊙O′的弦CE上,且不与C、E重合,
∴ 点 在⊙O′内.
在⊙O′内.
类似可求 (9,3).
(9,3).
显然,点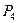 在点E的右侧,
在点E的右侧,
∴点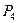 在⊙O′外.
在⊙O′外.
当OA=OP时,同①可求得,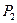 (4,3),
(4,3),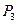 (-4,3).
(-4,3).
显然,点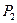 在点E的右侧,点
在点E的右侧,点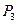 在点C的左侧
在点C的左侧
因此,在直线BC上,除了E点外,还存在点 ,
, 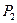 ,
,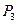 ,
,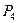 ,它们分别使△AOP为等腰三角形,且点
,它们分别使△AOP为等腰三角形,且点 在⊙O′内,点
在⊙O′内,点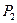 、
、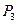 、
、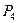 在⊙O′外.
在⊙O′外.  …………7分
…………7分
依题意得,x(x+2)=15.
解得
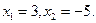 (不合题意,舍去)
(不合题意,舍去)∴ OC="3" ,OA="5" . …………………………………1分
(2)证明:连结O′D,在矩形OABC中,

∵ OC=AB,∠OCB=∠ABC,E为BC的中点,
∴△OCE≌△ABE .
∴ EO="EA" .
∴∠EOA=∠EAO .
又∵O′O= O′D,
∴ ∠O′DO=∠EOA=∠EAO.
∴ O′D∥EA .
∵ DF⊥AE,
∴ DF⊥O′D .
又∵点D在⊙O′上,O′D为⊙O′的半径,
∴ DF为⊙O′的切线. …………………………………3分
(3)答:存在 .
当OA=AP时,以点A为圆心,以AO为半径画弧,交BC于点
 和
和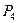 两点,
两点,则△AO
 、△AO
、△AO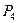 均为等腰三角形.
均为等腰三角形.证明:过
 点作
点作 H⊥OA于点H,则
H⊥OA于点H,则 H=OC=3,
H=OC=3,∵ A
 =OA=5,
=OA=5,∴ AH=4,OH=1.
∴
 (1,3).
(1,3).∵
 (1,3)在⊙O′的弦CE上,且不与C、E重合,
(1,3)在⊙O′的弦CE上,且不与C、E重合,∴ 点
 在⊙O′内.
在⊙O′内.类似可求
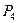 (9,3).
(9,3).显然,点
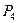 在点E的右侧,
在点E的右侧,∴点
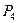 在⊙O′外.
在⊙O′外.当OA=OP时,同①可求得,
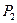 (4,3),
(4,3),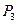 (-4,3).
(-4,3).显然,点
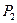 在点E的右侧,点
在点E的右侧,点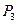 在点C的左侧
在点C的左侧因此,在直线BC上,除了E点外,还存在点
 ,
, 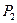 ,
,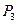 ,
,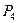 ,它们分别使△AOP为等腰三角形,且点
,它们分别使△AOP为等腰三角形,且点 在⊙O′内,点
在⊙O′内,点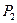 、
、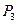 、
、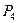 在⊙O′外.
在⊙O′外.  …………7分
…………7分略

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
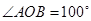 ,点C在
,点C在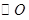 上,且点C不与A、B重合,则
上,且点C不与A、B重合,则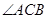 的度数为( )
的度数为( )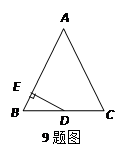
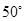 B.
B.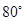 或
或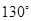 D.
D. (1)求证: ;
(1)求证: ;
 的半径为
的半径为 ,圆心
,圆心 的距离为
的距离为 ,则直线
,则直线 )
) 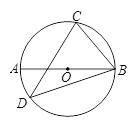




 内接于⊙O,
内接于⊙O, 是⊙O的切线,
是⊙O的切线, 的延长线交
的延长线交 .
.
 ,求⊙O的半径
,求⊙O的半径