题目内容
【题目】在一条笔直的公路上有A、B两地，甲骑自行车从A地到B地；乙骑摩托车从B地到A地，到达A地后立即按原路返回．如图是甲、乙两人离B地的距离y（km）与行驶时间x（h）之间的函数图象，根据图象解答以下问题：
（1）直接写出y甲，y乙与x之间的函数关系式（不写过程）；
（2）①求出点M的坐标，并解释该点坐标所表示的实际意义；
②根据图象判断，x取何值时，y乙＞y甲．
【答案】（1）y甲=﹣10x+20，y乙=﹣20x+40；（2）①M（
，
）．表示小时时两车相遇，此时距离B地千米．②＜x＜2时，y乙＞y甲．
【解析】
(1)对图象进行点标注，结合图象得到相关点的坐标；利用待定系数法求出AB所在直线以及OC所在直线的函数解析式，进而建立方程组即可解答.
(2)观察图像即可解答.
解：（1）设甲离B地的距离y（km）与行驶时间x（h）的函数关系式为y=kx+b，
把（0，20），（2，0）代入得：
，
解得：
，
∴y甲=﹣10x+20．
同法可得当0＜x≤1时，y乙=20x，当1＜x≤2时，y乙=﹣20x+40，
（2）①由
，解得
∴M（
，
）．
表示小时时两车相遇，此时距离B地千米．
②观察图象可知：＜x＜2时，y乙＞y甲．
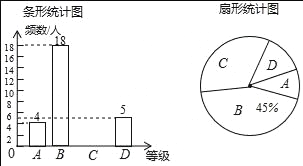
小学夺冠AB卷系列答案
【题目】2018年10月17日是我国第五个“扶贫日”,某校学生会干部对学生倡导的“扶贫”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图所示的统计图,(图中信息不完整)，已知A.B两组捐款人数的比为1:5.
被调查的捐款人数分组统计表：
组别 | 捐款额x/元 | 人数 |
A | 1≤x＜10 | a |
B | 10≤x＜20 | 100 |
C | 20≤x＜30 | ______ |
D | 30≤x＜40 | ______ |
E | 40≤x | ______ |
请结合以上信息解答下列问题：
(1)求a的值和参与调查的总人数；
(2)补全“被调查的捐款人数分组统计图1”并计算扇形B的圆心角度数；
(3)已知该校有学生2200人，请估计捐款数不少于30元的学生人数有多少人?
