��Ŀ����
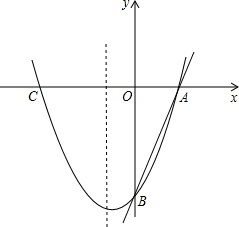
������y=a��x+6��2-3��x���ཻ��A��B���㣬��y���ཻ��C��DΪ�����ߵĶ��㣬ֱ��DE��x�ᣬ����ΪE��AE2=3DE��
��1������������ߵĽ���ʽ��
��2��PΪֱ��DE�ϵ�һ���㣬��PCΪб�߹���ֱ�������Σ�ʹֱ�Ƕ�������x���ϣ�����x���ϵ�ֱ�Ƕ���ֻ��һ��ʱ�����P�����ꣻ
��3��MΪ�������ϵ�һ���㣬��M��ֱ��MN��DM����ֱ��DE��N����M���������ߵĵڶ����IJ������˶�ʱ���Ƿ����ʹ��E���ȷ��߶�DN������������ڣ���������з���������M�����ꣻ�������ڣ���˵�����ɣ�


��1������������ߵĽ���ʽ��
��2��PΪֱ��DE�ϵ�һ���㣬��PCΪб�߹���ֱ�������Σ�ʹֱ�Ƕ�������x���ϣ�����x���ϵ�ֱ�Ƕ���ֻ��һ��ʱ�����P�����ꣻ
��3��MΪ�������ϵ�һ���㣬��M��ֱ��MN��DM����ֱ��DE��N����M���������ߵĵڶ����IJ������˶�ʱ���Ƿ����ʹ��E���ȷ��߶�DN������������ڣ���������з���������M�����ꣻ�������ڣ���˵�����ɣ�


��1����֪�����ߵĶ���D��-6��-3������DE=3��OE=6��
��AE2=3DE=9��
��AE=3����A��-3��0����
��A��������������ߵĽ���ʽ�У�
�ã�a��-3+6��2-3=0��
��a=
��
�������ߵĽ���ʽΪ��y=
��x+6��2-3=
x2+4x+9��
��2�����P��-6��t������֪C��0��9����
��PC���е�Q��-3��
����
��֪��PC=
��
����PCΪб�߹���ֱ�������Σ���x���ϵ�ֱ�Ƕ���ֻ��һ��ʱ����PCΪֱ����Բ��x�����У�����
|
|=
��
���t=1��
�ʵ�P��-6��1����
����P���E�غ�ʱ���������ߵĽ���ʽ��֪��A��-3��0����B��-9��0����
����P��-6��0����
�ʵ�P������Ϊ��-6��1����-6��0����
��3�����M��a��b����a��0��b��0����������������ۣ�
�ٵ�NE=2DEʱ��NE=6����N��-6��6������֪D��-6��-3�������У�
ֱ��MN��б�ʣ�k1=
��ֱ��MD��б�ʣ�k2=
��
����MN��DM����k1•k2=
=-1��
�����ã�a2+b2+12a-3b+18=0����������
�������ߵĽ���ʽ�ã�
a2+4a+9=b��
�����ã�a2+12a-3b+27=0����������
������-�������ã�b2=9����b=3����ֵ��ȥ����
��b=3���루�����ã�a=-6+3
��a=-6-3
��
�ʵ�M��-6+3
��3����-6-3
��3����
�ڵ�2NE=DEʱ��NE=
����N��-6��
������֪D��-6��-3����
���У�ֱ��MN��б�ʣ�k1=
��ֱ��DM��б�ʣ�k2=
��
������ã�k1•k2=
=-1��
�����ã�a2+b2+
b+12a+
=0��
��a2+12a-3b+27=0����ʽ�����
�ã�2b2+9b+9=0��
���b=-2��b=-
���������������⣬��ȥ����
���Ͽ�֪�����ڷ���������M�㣬������Ϊ��M��-6+3
��3����-6-3
��3����
��AE2=3DE=9��
��AE=3����A��-3��0����
��A��������������ߵĽ���ʽ�У�
�ã�a��-3+6��2-3=0��
��a=
| 1 |
| 3 |
�������ߵĽ���ʽΪ��y=
| 1 |
| 3 |
| 1 |
| 3 |
��2�����P��-6��t������֪C��0��9����
��PC���е�Q��-3��
| 9+t |
| 2 |
��֪��PC=
| 36+(9-t)2 |
����PCΪб�߹���ֱ�������Σ���x���ϵ�ֱ�Ƕ���ֻ��һ��ʱ����PCΪֱ����Բ��x�����У�����
|
| 9+t |
| 2 |
| 1 |
| 2 |
| 36+(9-t)2 |
���t=1��
�ʵ�P��-6��1����
����P���E�غ�ʱ���������ߵĽ���ʽ��֪��A��-3��0����B��-9��0����
����P��-6��0����
�ʵ�P������Ϊ��-6��1����-6��0����
��3�����M��a��b����a��0��b��0����������������ۣ�
�ٵ�NE=2DEʱ��NE=6����N��-6��6������֪D��-6��-3�������У�
ֱ��MN��б�ʣ�k1=
| b-6 |
| a+6 |
| b+3 |
| a+6 |
����MN��DM����k1•k2=
| (b-6)(b+3) |
| (a+6)2 |
�����ã�a2+b2+12a-3b+18=0����������
�������ߵĽ���ʽ�ã�
| 1 |
| 3 |
�����ã�a2+12a-3b+27=0����������
������-�������ã�b2=9����b=3����ֵ��ȥ����
��b=3���루�����ã�a=-6+3
| 2 |
| 2 |
�ʵ�M��-6+3
| 2 |
| 2 |
�ڵ�2NE=DEʱ��NE=
| 3 |
| 2 |
| 3 |
| 2 |
���У�ֱ��MN��б�ʣ�k1=
b-
| ||
| a+6 |
| b+3 |
| a+6 |
������ã�k1•k2=
(b-
| ||
| (a+6)2 |
�����ã�a2+b2+
| 3 |
| 2 |
| 63 |
| 2 |
��a2+12a-3b+27=0����ʽ�����
�ã�2b2+9b+9=0��
���b=-2��b=-
| 3 |
| 2 |
���Ͽ�֪�����ڷ���������M�㣬������Ϊ��M��-6+3
| 2 |
| 2 |

��ϰ��ϵ�д�
�����Ŀ
 ���������BOF���ƣ������ڣ������P������ꣻ�������ڣ���˵�����ɣ�
���������BOF���ƣ������ڣ������P������ꣻ�������ڣ���˵�����ɣ�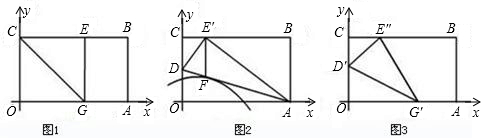
 ����x���ཻ�ڵ�F��
����x���ཻ�ڵ�F��
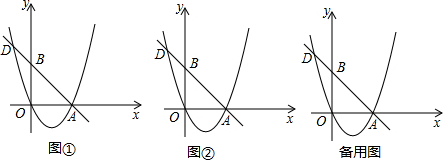
 A��D���㣬���������ཻ��B��1��m����C��2��2�����㣮
A��D���㣬���������ཻ��B��1��m����C��2��2�����㣮