��Ŀ����
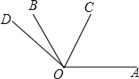
����Ŀ����ͼ1����P��Q�ֱ��DZ߳�Ϊ4cm�ĵȱߡ�ABC��AB��BC�ϵĶ��㣬��P�Ӷ���A����Q�Ӷ���Bͬʱ�����������ǵ��ٶȶ�Ϊ1cm/s�� 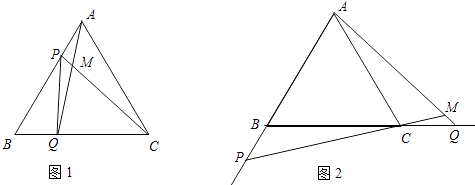
��1������AQ��CP���ڵ�M������P��Q�˶��Ĺ����У���CMQ�仯�����仯����˵�����ɣ������䣬��������Ķ�����
��2����ʱ��PBQ��ֱ�������Σ�
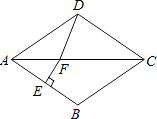
��3����ͼ2������P��Q���˶����յ�����������AB��BC���˶���ֱ��AQ��CP����ΪM�����CMQ�仯�����仯����˵�����ɣ������䣬��������Ķ�����
���𰸡�
��1���⣺��CMQ=60�㲻�䣮
�ߵȱ��������У�AB=AC����B=��CAP=60��
����������AP=BQ��
���ABQ�ա�CAP��SAS����
���BAQ=��ACP��
���CMQ=��ACP+��CAM=��BAQ+��CAM=��BAC=60��
��2���⣺��ʱ��Ϊt����AP=BQ=t��PB=4��t
�ٵ���PQB=90��ʱ��
�ߡ�B=60�㣬
��PB=2BQ����4��t=2t��t= ![]() ��
��
�ڵ���BPQ=90��ʱ��
�ߡ�B=60�㣬
��BQ=2BP����t=2��4��t����t= ![]() ��
��
�൱�� ![]() ����
���� ![]() ��ʱ����PBQΪֱ��������
��ʱ����PBQΪֱ��������
��3���⣺��CMQ=120�㲻�䣮
���ڵȱ��������У�BC=AC����B=��CAP=60��
���PBC=��ACQ=120�㣬
����������BP=CQ��
���PBC�ա�QCA��SAS��
���BPC=��MQC
�֡ߡ�PCB=��MCQ��
���CMQ=��PBC=180�㩁60��=120��
����������1����Ϊ��P�Ӷ���A����Q�Ӷ���Bͬʱ�����������ǵ��ٶȶ�Ϊ1cm/s������AP=BQ��AB=AC����B=��CAP=60�㣬������ñ߽DZ߶�����֪��ABQ�ա�CAP������ȫ�������ε����ʶ����������εĽǼ��ϵ�������ε���Ƕ����������CQM�Ķ�������2����ʱ��Ϊt����AP=BQ=t��PB=4��t���ֱ�͢ٵ���PQB=90��ʱ���ڵ���BPQ=90��ʱ����ֱ�������ε����ʶ������t��ֵ����3���������ñ߽DZ߶���֤�á�PBC�ա�QCA��������ȫ�������ε����ʶ����õ���BPC=��MQC�������������νǼ�Ĺ�ϵ��á�CMQ�Ķ�����
�����㾫����������Ҫ�����˵ȱ������ε����ʵ����֪ʶ�㣬��Ҫ���յȱ������ε������Ƕ���Ȳ���ÿ���Ƕ���60�������ȷ�����⣮

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�