题目内容
【题目】如图,方格纸中每个小方格都是边长为1的正方形,我们把以格点连线为边的多边形称为“格点多边形”,如图1中四边形ABCD就是一个“格点四边形”.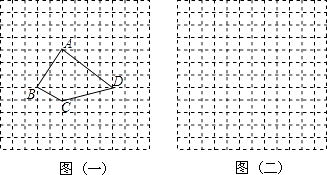
(1)求图1中四边形ABCD的面积;
(2)在图2方格纸中画一个格点三角形EFG,使△EFG的面积等于四边形ABCD的面积且为轴对称图形.
【答案】
(1)解:根据面积公式得:方法一:S= ![]() ×6×4=12;
×6×4=12;
方法二:S=4×6﹣ ![]() ×2×1﹣
×2×1﹣ ![]() ×4×1﹣
×4×1﹣ ![]() ×3×4﹣
×3×4﹣ ![]() ×2×3=12
×2×3=12
(2)解:(只要画出一种即可)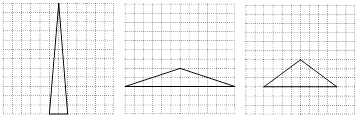

【解析】(1)不规则四边形面积可用作差法或求和法,转化为规则图形的面积之和或差;(2)由轴对称性,三角形需是等腰三角形,面积为12=![]() ,后面两个数可作为腰和底.
,后面两个数可作为腰和底.
【考点精析】解答此题的关键在于理解轴对称的性质的相关知识,掌握关于某条直线对称的两个图形是全等形;如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线;两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上.

练习册系列答案
相关题目