题目内容
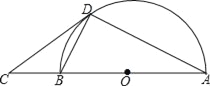
【题目】如图,AB是半圆O的直径,C是AB延长线上一点,CD与半圆O相切于点D,连接AD,BD.
(1)求证:∠BAD=∠BDC;
(2)若sin∠BDC=![]() ,BC=2,求⊙O的半径.
,BC=2,求⊙O的半径.
【答案】(1)证明见解析(2)3
【解析】
(1)连接OD,如图,先由切线的性质得∠ODB+∠BDC=90°,再由圆周角定理得到∠ODB+∠ODA=90°,则∠BDC=∠ODA,加上∠ODA=∠BAD,然后等量代换即可得到结论;
(2)利用正弦定义得sin∠A=sin∠BDC=![]() ,设BD=
,设BD=![]() x,AB=5x,则AD=2
x,AB=5x,则AD=2![]() x,然后证明△CBD∽△CDA,则利用相似比可计算出CD和AB,从而得到圆的半径.
x,然后证明△CBD∽△CDA,则利用相似比可计算出CD和AB,从而得到圆的半径.
(1)证明:连接OD,如图,
∵CD与半圆O相切于点D,
∴OD⊥CD,
∴∠ODC=90°,即∠ODB+∠BDC=90°,
∵AB是半圆O的直径,
∴∠BDA=90°,即∠ODB+∠ODA=90°,
∴∠BDC=∠ODA,
∵OD=OA,
∴∠ODA=∠BAD,
∴∠BAD=∠BDC;
(2)解:∵sin∠A=sin∠BDC=![]() ,
,
∴![]() ,
,
设BD=![]() x,AB=5x,则AD=
x,AB=5x,则AD=![]() =2
=2![]() x,
x,
∵∠BAD=∠BDC,∠BCD=∠DCA,
∴△CBD∽△CDA,
∴![]() ,
,
而BC=2,
∴CD=4,AC=8,
∴AB=AC﹣BC=6,
∴⊙O的半径位3.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目