题目内容
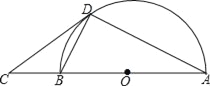
【题目】如图,AB是⊙O的直径,AC是弦,CD是⊙O的切线,C为切点,AD⊥CD于点D.
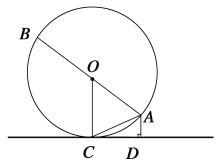
求证:(1)∠AOC=2∠ACD;(2)AC2=AB·AD.
【答案】(1)证明见解析;(2)证明见解析
【解析】
试题分析:(1)根据CD为切线得出∠ACD+∠ACO=90°,根据OC=OA得出∠ACO=∠CAO,即![]() ∠AOC+∠ACO=90°,将两式联立得出答案;(2)连接BC,根据AB为直径得出∠ACB=90°,结合∠AOC=2∠B得出∠B=∠ACD,从而得到△ACD∽△ABC,得出答案.
∠AOC+∠ACO=90°,将两式联立得出答案;(2)连接BC,根据AB为直径得出∠ACB=90°,结合∠AOC=2∠B得出∠B=∠ACD,从而得到△ACD∽△ABC,得出答案.
试题解析:(1)∵CD是⊙O的切线,∴∠OCD=90°, 即∠ACD+∠ACO=90°.…①
∵OC=OA,∴∠ACO=∠CAO, ∴∠AOC=180°-2∠ACO,即![]() ∠AOC+∠ACO=90°.…②
∠AOC+∠ACO=90°.…②
由①,②,得:∠ACD-![]() ∠AOC=0,即∠AOC=2∠ACD;
∠AOC=0,即∠AOC=2∠ACD;
(2)如图,连接BC.
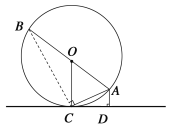
∵AB是直径,∴∠ACB=90° 在Rt△ACD与△RtABC中,∵∠AOC=2∠B,
∴∠B=∠ACD, ∴△ACD∽△ABC, ∴![]() =AB·AD
=AB·AD

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目