题目内容
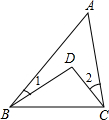
如图,AB∥EF,问∠A、∠C、∠1有何等量关系?证明你的结论.
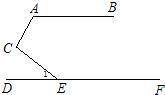

等量关系为:∠A+∠C-∠1=180°.
证明:
延长AC交EF于G,则∠ACE=∠2+∠1(三角形外角定理),
∵AB∥EF,
∴∠A+∠2=180°(两直线平行,同旁内角互补),
∠2=180°-∠A代入,∠ACE=180°-∠A+∠1,
即∠A+∠ACE-∠1=180°.
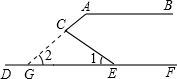
证明:
延长AC交EF于G,则∠ACE=∠2+∠1(三角形外角定理),
∵AB∥EF,
∴∠A+∠2=180°(两直线平行,同旁内角互补),
∠2=180°-∠A代入,∠ACE=180°-∠A+∠1,
即∠A+∠ACE-∠1=180°.


练习册系列答案
相关题目